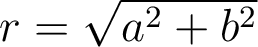Ressource - Nombres Complexes et trigonométrie
Conditions d’achèvement
Complexes - Trigonométrie
Ressources (pdf):
- Nombres complexes de module 1
- Les différentes représentations d’un nombre complexe
- Formule de Moivre et formule d’Euler
H- Ecriture trigonométrie
Définition 7. Soit
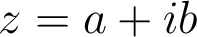 un nombre complexe de module
un nombre complexe de module 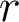 et d’argument
et d’argument 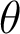 . On a vu que
. On a vu que 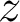 admet une unique écriture
algébrique et une unique écriture exponentielle. On peut montrer que
admet une unique écriture
algébrique et une unique écriture exponentielle. On peut montrer que 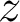 admet également une écriture trigonométrique (unique modulo
admet également une écriture trigonométrique (unique modulo 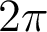 ) de la forme suivante :
) de la forme suivante : 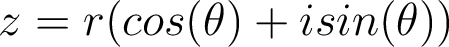 .
.Propriété. Le complexe
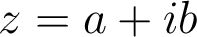 a pour forme exponentielle
a pour forme exponentielle 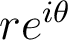 si et seulement si :
si et seulement si :