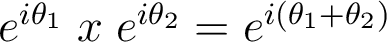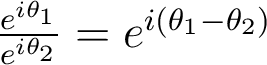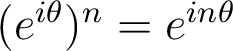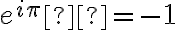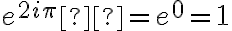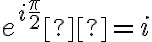Ressource - Nombres Complexes - Module, argument et écriture exponentielle
Completion requirements
Complexes - Ecriture exponentielle
E- Nombres complexes de module 1
Définition 6. Soit
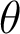 un réel. On définit l'exponentielle complexe
un réel. On définit l'exponentielle complexe 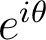 ou
ou 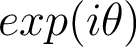 comme l'unique nombre complexe d'écriture algébrique :
comme l'unique nombre complexe d'écriture algébrique : 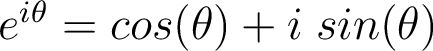 .
.Il s’agit de l’affixe du point
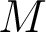 situé sur le cercle trigonométrique et tel que
situé sur le cercle trigonométrique et tel que 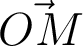 forme un angle avec l’axe réel. En particulier le module de
forme un angle avec l’axe réel. En particulier le module de 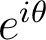 est
est 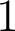 et
et 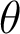 est un de ses arguments.
est un de ses arguments.
Réciproquement tous les nombres complexes de module
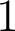 s’écrivent sous la forme d’une exponentielle complexe.
s’écrivent sous la forme d’une exponentielle complexe.
L’exponentielle complexe est une écriture pratique car ses propriétés sont les mêmes que celle de l’exponentielle réelle.
Propriétés. Si
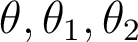 sont des réels et
sont des réels et 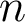 un entier positif :
un entier positif : Ces propriétés se visualisent aisément sur le cercle trigonométrique. En particulier on note les valeurs remarquables suivantes :
F- Ecriture exponentielle d'un nombre complexe
Définition 7. Soit
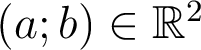 et
et 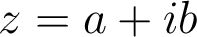 . Si
. Si 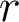 est le module de
est le module de 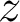 et
et
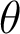 un de ses arguments, on peut montrer que
un de ses arguments, on peut montrer que 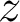 admet une écriture exponentielle (unique
admet une écriture exponentielle (unique 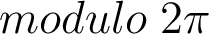 ) de la forme suivante :
) de la forme suivante : 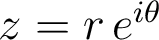 .
.
Cette écriture facilite grandement les calculs de produits et de puissance puisque l'on peut alors appliquer les propriétés de l'exponentielle complexe.