2. Évaluation géométrique de la FTI

2.1. Exemple : défaut de mise au point

Clarifions ce point en traitant l'exemple élémentaire du défaut de mise au point, qui permet une résolution analytique du problème :

  • On considère un système optique à pupille circulaire, travaillant dans une conjugaison quelconque, dont l'ouverture numérique image est  sin \alpha'_m .
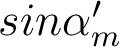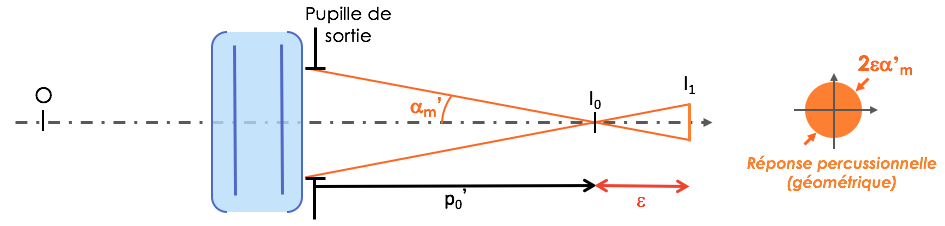
  • Le système est en limite de diffraction, mais l'imagerie est faite dans un plan éloigné du plan image paraxial : le défaut de mise au point longitudinal est ε.
  • La réponse percussionnelle, dans une description purement géométrique, est un disque homogène de rayon  \epsilon \times \alpha'_m .
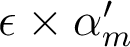  • Le défaut de mise au point est important, de sorte que le rayon de la tache aberrante est très supérieur à celui de la tache d'Airy :  \epsilon \times \alpha'_m \ \gg \frac{1,22 \lambda }{2 \alpha'_m}


Par définition, la fonction de transfert du système optique est la transformée de Fourier de la RPI : dans le cas présent, la RPI est une fonction disque et sa transformée de Fourier n'est rien d'autre que la fonction de Bessel  \frac{2J_1 (2\pi \sigma' \times \epsilon\alpha'_m ) }{2\pi \sigma' \times \epsilon\alpha'_m } .

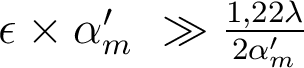
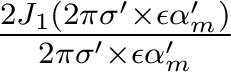La figure ci-dessous représente cette évaluation géométrique de la FTI pour deux défauts de mise au point d'amplitude 2 λ et 4 λ respectivement (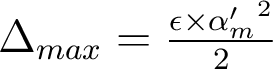 \Delta_{max} = \frac{\epsilon \times {\alpha'_m}^2 }{2} ). Dans ce cas, l'approche géométrique conduit à une expression analytique de la FTI, que l'on compare à la simulation numérique de la FTI (avec diffraction). Il apparaît que les deux descriptions sont tout à fait concordantes, et que la description purement géométrique de la FTI est valable dans ce contexte.


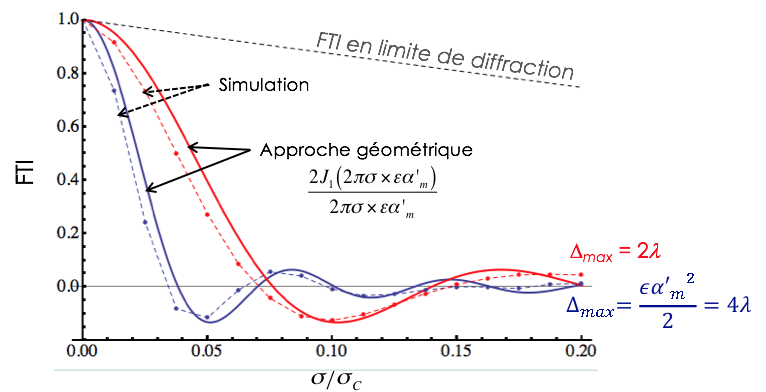
Comparaison des descriptions géométrique et complète de la FTI en présence d'un défaut de mise au point

La FTI fait ici clairement apparaître les inversions de contraste caractéristiques d'un défaut de mise au point important.

Exercice d'application

Pour approfondir cette analyse, demandons-nous :

  1. quel est le diamètre de la tache de diffusion aberrante pour Δmax = 4 λ ? 
  2. quelle est la fréquence spatiale associée au 1er zéro de la FTI géométrique ?
  3. comment se compare la période de la mire associée à ce zéro par rapport à la tache d'Airy ?

Les applications numériques seront faites pour 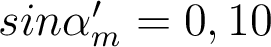 sin \alpha'_m = 0,10 à λ = 0,5 µm. Corrections à la fin de ce chapitre.