Cours n°12 : Fonction de Transfert Optique
| Site: | eCampus |
| Cours: | 7P-138-PHO - Conception de Systèmes Optiques |
| Livre: | Cours n°12 : Fonction de Transfert Optique |
| Imprimé par: | Visiteur anonyme |
| Date: | mardi 10 mars 2026, 09:56 |
Description
Complément au cours sur la fonction de transfert optique en éclairage incohérent (FTI = FTO)
1. Système optique présentant une obturation centrale
Les systèmes à miroirs, type télescopes, présentent en général une obturation centrale. Dans ces conditions, la pupille n'est pas un disque plein mais un anneau. La réponse percussionnelle associée en limite de diffraction est modifiée (cf. Cours n°3), la fonction de transfert également par conséquent. C'est ce que montre la figure ci-dessous :
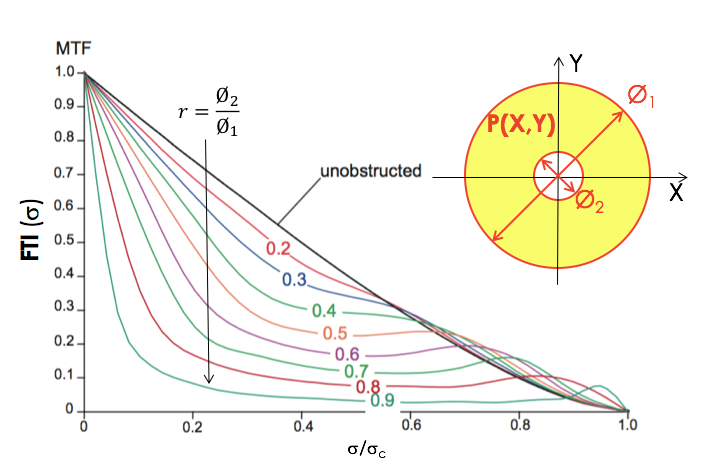
Evolution de la fonction de transfert de modulation avec l'obturation centrale (définie par le ratio 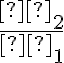 ) [Handbook of Optical Systems IV, ed. H. Gross]
) [Handbook of Optical Systems IV, ed. H. Gross]
En comparaison du système à pupille pleine (r = 0), on peut noter que :
- la fréquence de coupure extrême - au-delà de laquelle la fonction de transfert est nulle -
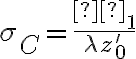 est inchangée ;
est inchangée ; - la détérioration du contraste est forte aux fréquences spatiales intermédiaires ;
- le contraste est amélioré près de la fréquence de coupure.
Il est important de remarquer que ce dernier point ne remet pas en cause le résultat suivant lequel la valeur de la FTI aberrante ne peut être supérieure à celle du même système en limite de diffraction : nous ne comparons ici que des dispositifs en limite de diffraction, dont les pupilles sont toutes différentes. Toutefois, cela explique l'intérêt qu'une illumination annulaire peut présenter dans certains dispositifs de microscopie recherchant une résolution améliorée.
2. Évaluation géométrique de la FTI
On peut se demander si la définition de la FTI, telle que faite en cours, implique intrinsèquement de prendre en compte la diffraction - de manière analogue à la définition de la RPI. Il n'en est rien : la fonction de transfert est une notion plus générale que l'approche choisie pour l'évaluer. C'est une grandeur qui mesure le contraste de l'image d'une mire, en fonction de sa fréquence spatiale. Ainsi, il n'est pas strictement indispensable de prendre en compte la diffraction pour l'évaluer.
Pour un système optique très aberrant, la RPI évaluée en prenant en compte la diffraction est en fait très différente d'une tache d'Airy, et nettement plus étendue. On peut évaluer la dimension de la tache aberrante de manière purement géométrique par un tracé de rayons (diagramme de points). La FTI peut ainsi être calculée en appliquant sa définition, à savoir la transformée de Fourier de la réponse percussionnelle décrite géométriquement.
Il est clair que cette description ne pourra rendre compte que du comportement d'un système optique très aberrant, aux basses fréquences spatiales éloignées de celle limitée par la diffraction.
2.1. Exemple : défaut de mise au point
Clarifions ce point en traitant l'exemple élémentaire du défaut de mise au point, qui permet une résolution analytique du problème :
- On considère un système optique à pupille circulaire, travaillant dans une conjugaison quelconque, dont l'ouverture numérique image est
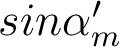 .
. - Le système est en limite de diffraction, mais l'imagerie est faite dans un plan éloigné du plan image paraxial : le défaut de mise au point longitudinal est ε.
- La réponse percussionnelle, dans une description purement géométrique, est un disque homogène de rayon
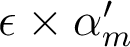 .
. - Le défaut de mise au point est important, de sorte que le rayon de la tache aberrante est très supérieur à celui de la tache d'Airy :
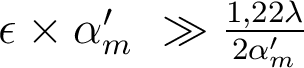
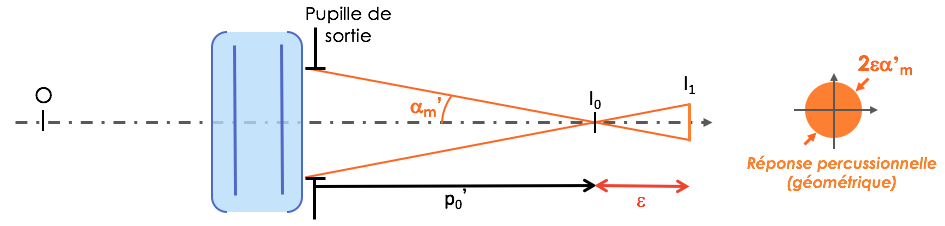
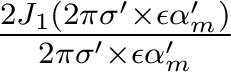 .
.La figure ci-dessous représente cette évaluation géométrique de la FTI pour deux défauts de mise au point d'amplitude 2 λ et 4 λ respectivement (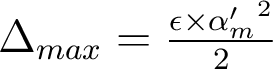 ). Dans ce cas, l'approche géométrique conduit à une expression analytique de la FTI, que l'on compare à la simulation numérique de la FTI (avec diffraction). Il apparaît que les deux descriptions sont tout à fait concordantes, et que la description purement géométrique de la FTI est valable dans ce contexte.
). Dans ce cas, l'approche géométrique conduit à une expression analytique de la FTI, que l'on compare à la simulation numérique de la FTI (avec diffraction). Il apparaît que les deux descriptions sont tout à fait concordantes, et que la description purement géométrique de la FTI est valable dans ce contexte.
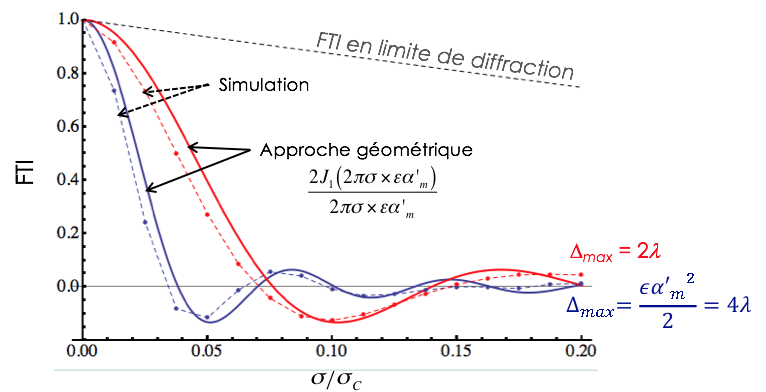
Comparaison des descriptions géométrique et complète de la FTI en présence d'un défaut de mise au point
La FTI fait ici clairement apparaître les inversions de contraste caractéristiques d'un défaut de mise au point important.
Exercice d'application
Pour approfondir cette analyse, demandons-nous :
- quel est le diamètre de la tache de diffusion aberrante pour Δmax = 4 λ ?
- quelle est la fréquence spatiale associée au 1er zéro de la FTI géométrique ?
- comment se compare la période de la mire associée à ce zéro par rapport à la tache d'Airy ?
Les applications numériques seront faites pour 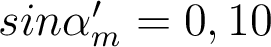 à λ = 0,5 µm. Corrections à la fin de ce chapitre.
à λ = 0,5 µm. Corrections à la fin de ce chapitre.
2.2. Conclusions
Quelques remarques conclusives sur la description géométrique de la FTI :
- c'est une approche légitime en présence de fortes aberrations - dans le même cadre de validité que l'analyse de la réponse percussionnelle à partir du diagramme de points ;
- la FTI évaluée de cette façon ne peut rendre compte que du comportement aux basses fréquences spatiales, c'est-à-dire aux fréquences
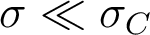 . En effet, la fréquence de coupure
. En effet, la fréquence de coupure 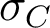 est explicitement associée à la limite de diffraction ... qui n'est pas prise en compte ici !
est explicitement associée à la limite de diffraction ... qui n'est pas prise en compte ici ! - la FTI est simulée en calculant la transformée de Fourier de la réponse percussionnelle.
- la relation entre FTI et autocorrélation de la pupille a été démontrée à partir de la RPI avec prise en compte de la diffraction - cela ne correspond donc pas à l'étude faite ici.
3. Fonction de transfert pour mire rectangulaire
La fonction de transfert de modulation ( = module de la fonction de transfert optique/incohérente), dans sa définition même, donne accès au contraste de l'image d'une mire d'éclairement sinusoïdal en fonction de sa fréquence spatiale - c'est-à-dire qu'elle s'intéresse à des mires ne contenant qu'une seule fréquence spatiale. Bien qu'une mire sinusoïdale ait une expression analytique très simple, sa réalisation expérimentale est plus complexe. Au contraire, les mires à profil d'éclairement rectangulaire (autrement dit, des traits alternativement noirs et blancs) sont très simples à réaliser, et d'un usage courant pour la caractérisation des dispositifs optiques. C'est pourquoi il est souvent utile de s'intéresser à la fonction de transfert rectangulaire (Square Transfer Function), que les logiciels calculent aisément, et qui est directement comparable aux observations expérimentales.
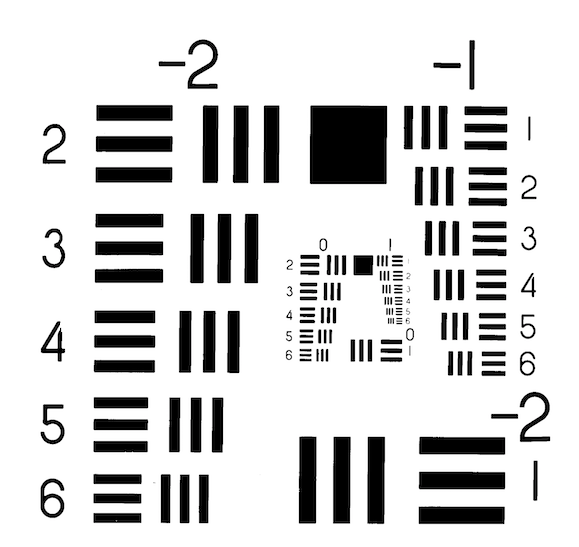
Mire de test à profils rectangulaires (mire USAF de référence)
En effet, l'éclairement d'une mire à profil rectangulaire, de période a, se décompose en série de Fourier :
Il est donc élémentaire d'en déduire l'éclairement de l'image à partir des valeurs de la fonction de transfert 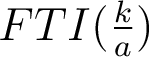 appliquées à chacune des composantes (cf. cours). On peut alors exprimer le contraste de la mire rectangulaire de période a, qui est par définition la FTR à la fréquence spatiale
appliquées à chacune des composantes (cf. cours). On peut alors exprimer le contraste de la mire rectangulaire de période a, qui est par définition la FTR à la fréquence spatiale  :
:
soit
La fonction de transfert rectangulaire donne donc le contraste de l'image de la mire en fonction de sa fréquence fondamentale  . La figure ci-dessous compare les fonctions de transfert en limite de diffraction d'un objectif à pupille circulaire homogène : le contraste de l'image de la mire rectangulaire de période a est supérieur à celui de l'image de la mire sinusoïdale.
. La figure ci-dessous compare les fonctions de transfert en limite de diffraction d'un objectif à pupille circulaire homogène : le contraste de l'image de la mire rectangulaire de période a est supérieur à celui de l'image de la mire sinusoïdale.
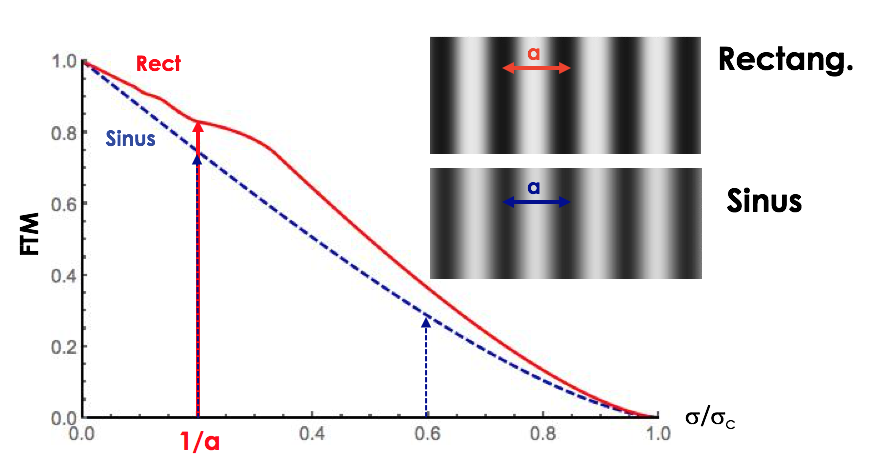
Module des fonctions de transfert pour une mire sinusoïdale et rectangulaire, pour un dispositif optique en limite de diffraction à pupille circulaire homogène
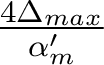
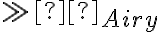
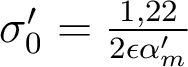
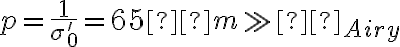
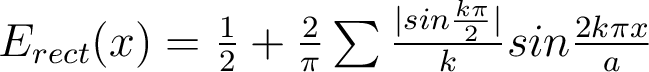
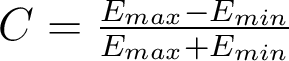
![FT_{Rect}(\frac{1}{a})= \frac{4}{\pi} \sum{\frac{-sin \frac{k\pi}{2}}{k} \times FTM(\frac{k}{a})}= \frac{4}{\pi} \times [FTM(\frac{1}{a})- \frac{1}{3}FTM(\frac{3}{a}) + \frac{1}{5}FTM(\frac{5}{a}) -...] FT_{Rect}(\frac{1}{a})= \frac{4}{\pi} \sum{\frac{-sin \frac{k\pi}{2}}{k} \times FTM(\frac{k}{a})}= \frac{4}{\pi} \times [FTM(\frac{1}{a})- \frac{1}{3}FTM(\frac{3}{a}) + \frac{1}{5}FTM(\frac{5}{a}) -...]](https://ecampus.paris-saclay.fr/filter/tex/pix.php/44c580ad5c5181a89f456e8827a5dc39.png)