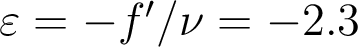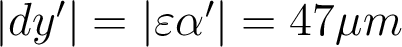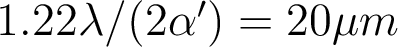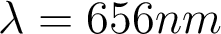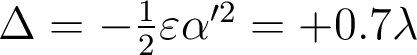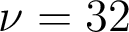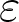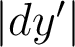Exercice : Chromatisme primaire d'une lentille mince (cours CSO 4)
Completion requirements
Exercices d'application sur le chromatisme
2. Réponses
Chromatisme axial
Chromatisme latéral
- Pour annuler le chromatisme latéral il faut placer la pupille sur la lentille, car c'est pour cette position que le rayon moyen ne sera pas dévié, pour aucune longueur d'onde.
- a)
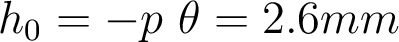 , en prenant
, en prenant 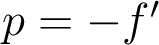 la position de la pupille
la position de la pupille
b)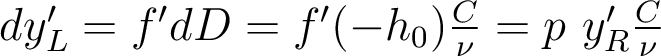 . Sur cette expression générale on voit que le chromatisme latéral dépend de la position de la pupille, et s'annule pour
. Sur cette expression générale on voit que le chromatisme latéral dépend de la position de la pupille, et s'annule pour 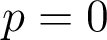 . Pour
. Pour  , on trouve
, on trouve 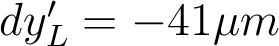 .
.
c)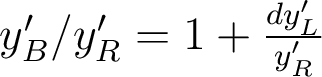 : l'image bleue est plus petite que l'image rouge, de
: l'image bleue est plus petite que l'image rouge, de 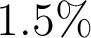 .
.
d) L'écart normal associé au chromatisme latéral est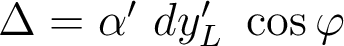 . En bord de pupille et pour
. En bord de pupille et pour 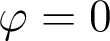 , il vaut
, il vaut 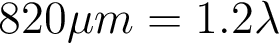 .
.
e) L'écart normal associé globalement au chromatisme (axial et latéral) vaut donc, en bord de pupille et pour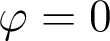 :
: 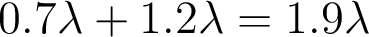 .
. - Lorsqu'on passe maintenant à du SF5 (
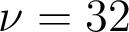 ),
), 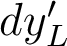 est multiplié par 2, ainsi que l'écart normal associé.
est multiplié par 2, ainsi que l'écart normal associé.