Cours n°3 : Réponse percussionnelle

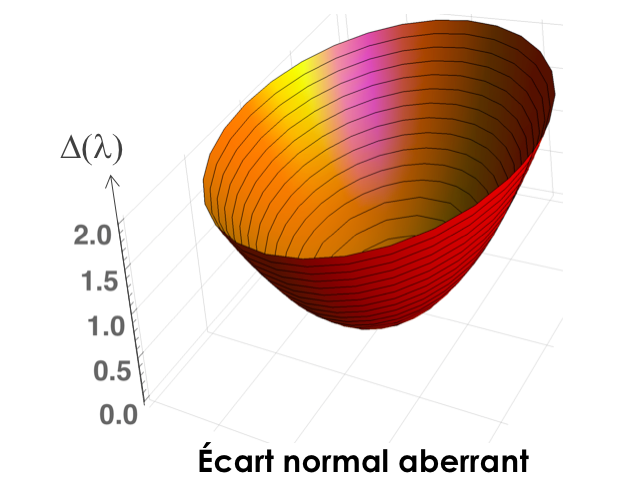
Je vous propose de comparer la description purement géométrique des aberrations à celle qui prend en compte la diffraction, dans l'exemple simple d'un défaut de mise au point ε, pour un système travaillant à la longueur d'onde λ = 0,78 µm et une ouverture numérique 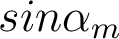$sin \alpha_m$ = 0,20. L'écart normal aberrant associé est $\Delta(\alpha,\varphi) = 2\lambda \times \frac{\alpha^2}{\alpha_m^2}$.

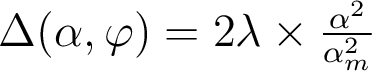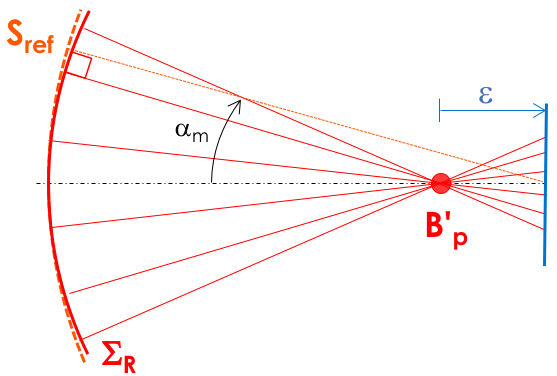
• Déterminez la forme et le diamètre du spot-diagramme, dans une approche purement géométrique. Ce système est-il en limite de diffraction ?
  
• Pouvez-vous en déduire l'amplitude du défaut de mise au point ε ?
• L'estimation approchée du rapport de Strehl est-elle possible ? Commentez.