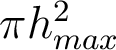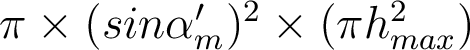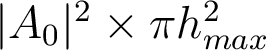Cours n°3 : Réponse percussionnelle

Site:	eCampus
Cours:	7P-138-PHO - Conception de Systèmes Optiques
Livre:	Cours n°3 : Réponse percussionnelle

Imprimé par:	Visiteur anonyme
Date:	jeudi 18 septembre 2025, 21:40

Description

Complément au cours n°3 sur la réponse percussionnelle incohérente

Table des matières

1. Réponse percussionnelle en limite de diffraction
- 1.1. Profils d'éclairement
- 1.2. Maximum d'éclairement
2. Étude de cas

1. Réponse percussionnelle en limite de diffraction

La réponse percussionnelle incohérente (RPI) décrit le profil d'éclairement correspondant à l'image d'un point, en prenant en compte la diffraction - c'est-à-dire le fait que la pupille a une dimension limitée. Cette approche repose sur l'optique de Fourier, dans le cadre de la diffraction de Fresnel. Le terme incohérent fait ici référence au fait que l'éclairage est spatialement incohérent, et donc que deux points adjacents dans l'image n'interfèrent pas : les éclairements se somment, non les champs optiques.

Dans ce cadre, la RPI est simplement proportionnelle au module carré de la transformée de Fourier de la fonction 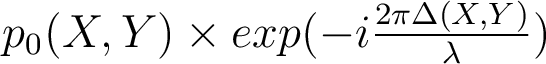$p_0(X,Y) \times exp (-i \frac{2\pi \Delta(X,Y)}{\lambda} )$ .

1.1. Profils d'éclairement

Le profil d'éclairement de la réponse percussionnelle (RPI) en limite de diffraction dépend de la forme de la pupille : dans les cas usuels pour les systèmes optiques à symétrie de révolution, la pupille est un disque homogène, et la RPI est alors une tache d'Airy. Par contre, pour des télescopes, l'obturation centrale conduit à une pupille annulaire, et la RPI en limite de diffraction est sensiblement modifiée : les anneaux sont plus marqués, et le maximum d'éclairement diminue relativement.

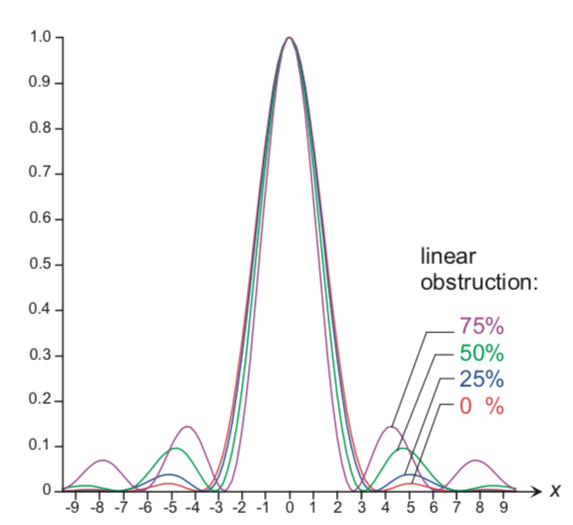
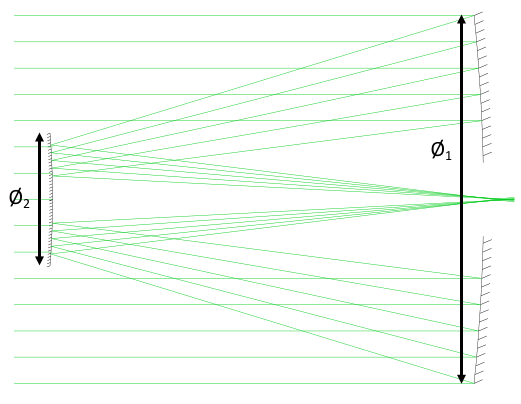
Évolution du profil d'éclairement de la RPI en limite de diffraction, en fonction de l'obturation centrale définie par le ratio 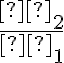$\frac{Ø_2}{Ø_1}$ des Ø de l'anneau (Handbook of Optical Systems IV, ed. H. Gross) ; ici les RPI sont toutes normalisées, ce qui ne met pas en évidence la réduction de l'éclairement au centre de la tache.

De même, pour une optique utilisée avec un faisceau laser, la pupille aura plutôt un profil gaussien - correspondant au profil du faisceau lumineux incident ; dans ce cas, la RPI en limite de diffraction est une gaussienne dont le diamètre à 1/e² est 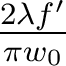$\frac{2 \lambda f'}{\pi w_0}$ avec w₀ le rayon de waist dans la pupille - soit encore 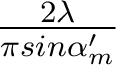$\frac{2 \lambda}{\pi sin \alpha'_m}$ pour faire l'analogie avec l'expression du diamètre de la tache d'Airy.

1.2. Maximum d'éclairement

Dans le cas d'une pupille circulaire éclairée de manière homogène, la réponse percussionnelle en limite de diffraction suit le profil suivant :

(en reprenant les notations du cours)

Cette expression fait explicitement apparaître l'expression de l'éclairement maximal au centre de la tache d'Airy

$E_{max}= (\frac{|A_0|}{\lambda z_0})^2 \times (\pi h_{max}^2)^2$ .

Il est intéressant de remarquer que l'éclairement maximal varie comme la puissance 4 de l'ouverture numérique (

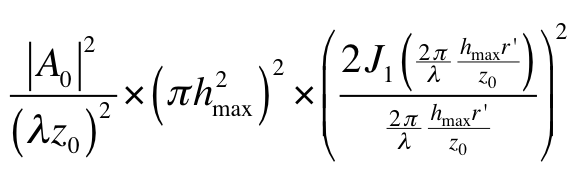
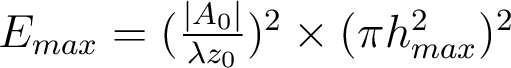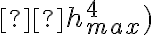$h_{max}^4)$ . Ceci découle d'une part du fait que le diamètre de la tache d'Airy diminue, et d'autre part du fait que le flux lumineux récupéré par le système augmente avec

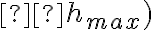$h_{max})$ - il est donc "quadruplement" bénéfique de chercher à augmenter l'ouverture numérique d'un système optique ... à condition de pouvoir assurer qu'il travaille en limite de diffraction et ne soit pas limité par les aberrations !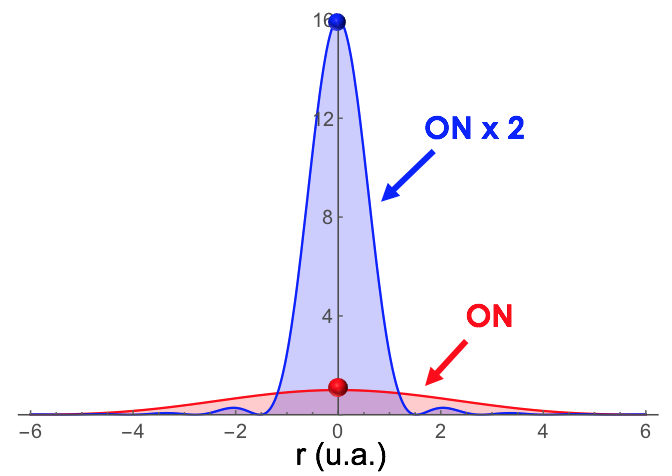

Cette dépendance avec l'ouverture numérique du système peut encore s'exprimer sous une forme différente :

$E_{max}= \frac{|A_0|^2}{\lambda^2} \times [\pi\times (\pi h_{max}^2)\times (sin\alpha'_m)^2]$ , où

$\pi h_{max}^2$ est la surface de la pupille, et donc

$\pi\times (sin\alpha'_m)^2 \times (\pi h_{max}^2)$ est l'étendue géométrique du faisceau (en sr.m²).

$|A_0|^2 \times \pi h_{max}^2$ est le flux lumineux qui traverse le système optique (en W).

2. Étude de cas

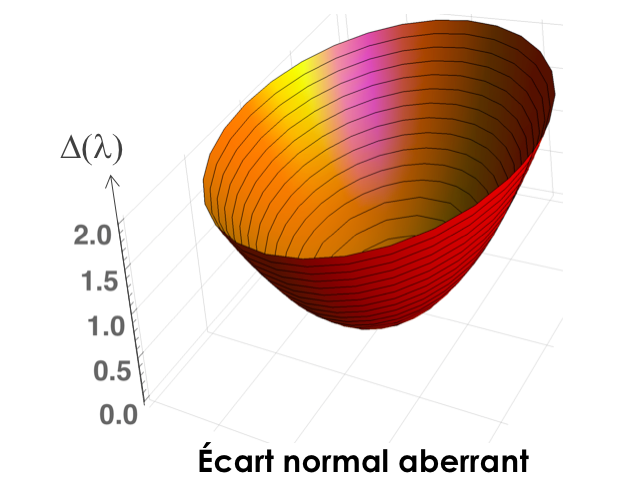
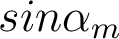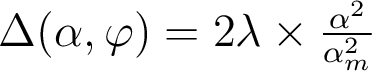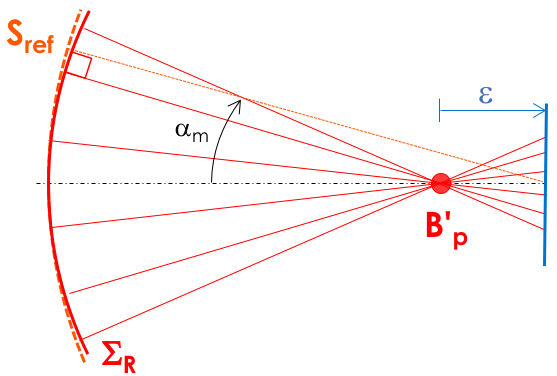
Je vous propose de comparer la description purement géométrique des aberrations à celle qui prend en compte la diffraction, dans l'exemple simple d'un défaut de mise au point ε, pour un système travaillant à la longueur d'onde λ = 0,78 µm et une ouverture numérique $sin \alpha_m$ = 0,20. L'écart normal aberrant associé est $\Delta(\alpha,\varphi) = 2\lambda \times \frac{\alpha^2}{\alpha_m^2}$ .

Déterminez la forme et le diamètre du spot-diagramme, dans une approche purement géométrique. Ce système est-il en limite de diffraction ?
Pouvez-vous en déduire l'amplitude du défaut de mise au point ε ?
L'estimation approchée du rapport de Strehl est-elle possible ? Commentez.

Je propose une solution détaillée de ce problème dans la vidéo ci-dessous :