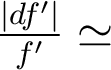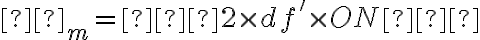Exercice : Aberrations sur l'axe d'une lentille simple (CSO n°2)
Completion requirements
Exercice d'application autour de l'écart normal et des relations de Nijboer
2. Solution
- ON = 0,15
- ØA = 4,8 µm
-
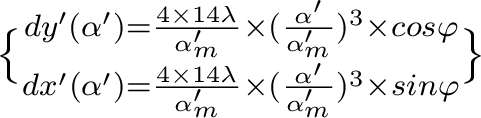
→ attention à l'application correcte des relations de Nijboer, qui font apparaître la dérivée partielle de l'écart normal par rapport à l'ouverture numérique α'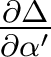 - et non par rapport à l'ouverture numérique normalisée
- et non par rapport à l'ouverture numérique normalisée 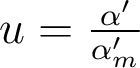
- tache-image à symétrie de révolution, avec un centre lumineux et un fond diffus
- Øm = 439 µm
- Les deux effets se cumulent ! L'aberration sphérique est sensiblement la même à toutes les longueurs d'onde. Dans le plan de mise au point rouge, on observe une tache de diffusion dont le diamètre est proche de la somme des deux contributions,
avec un bord diffus dans le bleu associé à l'aberration sphérique défocalisée à cette longueur d'onde.
La simulation ci-dessous représente le diagramme de points dans le plan de mise au point rouge de la lentille. Le diamètre total est un peu plus faible que celui estimé ici car l'aberration sphérique aux trois longueurs d'onde n'est pas tout à fait aussi forte que celle considérée ici.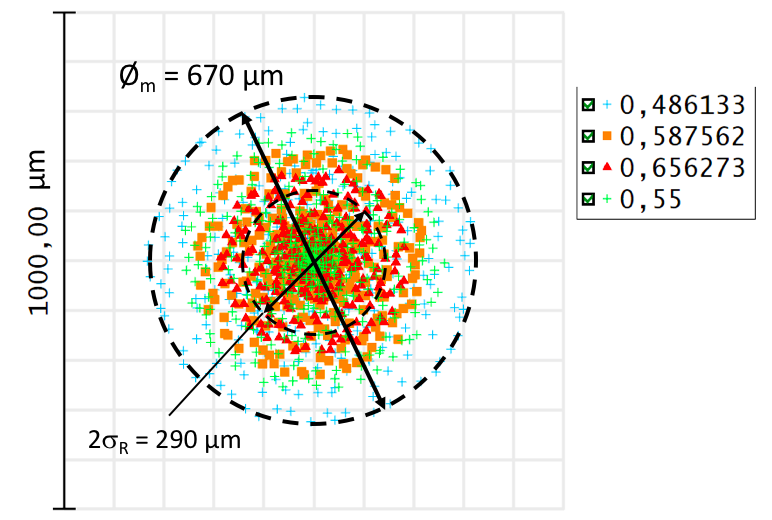
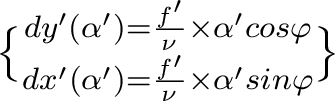 → le diamètre de la tache de diffusion bleue dans le plan de mise au point rouge est
→ le diamètre de la tache de diffusion bleue dans le plan de mise au point rouge est 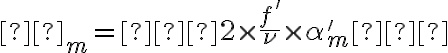 , idem que plus haut.
, idem que plus haut.