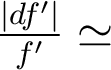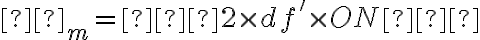Exercice : Aberrations sur l'axe d'une lentille simple (CSO n°2)
| Site: | eCampus |
| Course: | 7P-138-PHO - Conception de Systèmes Optiques |
| Book: | Exercice : Aberrations sur l'axe d'une lentille simple (CSO n°2) |
| Printed by: | Guest user |
| Date: | Tuesday, 10 March 2026, 9:57 AM |
Description
Exercice d'application autour de l'écart normal et des relations de Nijboer
1. Sujet
On s'intéresse à une lentille simple plan-convexe en BK7, de focale f' = 60 mm et de diamètre 18 mm, travaillant en conjugaison infini-foyer.
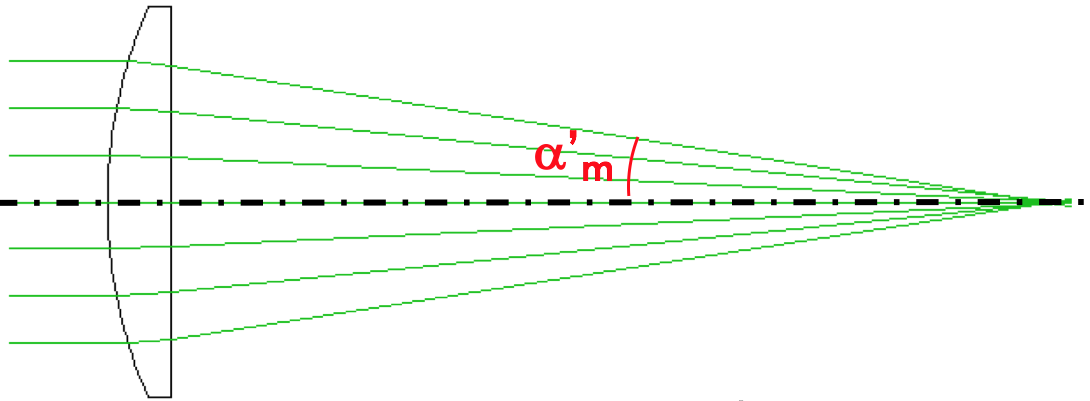
- Quelle est l'ouverture numérique
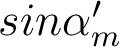 pour laquelle travaille cette lentille, dans la conjugaison considérée ?
pour laquelle travaille cette lentille, dans la conjugaison considérée ? - Quel est le diamètre de la tache d'Airy, à λ = 588 nm ?
- Pour un point objet sur l'axe, cette lentille présente de l'aberration sphérique caractérisée par un écart normal aberrant
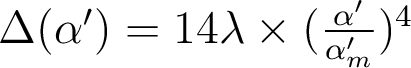 à λ = 588 nm qui mesure l'écart entre la surface d'onde
réelle et une surface de référence centrée sur l'image paraxiale.
à λ = 588 nm qui mesure l'écart entre la surface d'onde
réelle et une surface de référence centrée sur l'image paraxiale. - A l'aide des relations de Nijboer, exprimez les aberrations transverses dx'(α') et dy'(α'), coordonnées d'un point d'impact dans le plan image paraxial d'un rayon d'angle d'ouverture α'.
- Quelle est la forme du spot-diagramme ?
- Quel est son diamètre maximal ? Comparez à la tache d'Airy.
- On s'intéresse à présent au chromatisme longitudinal de cette lentille.
- Quelle est la distance
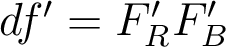 entre les foyers paraxiaux dans le bleu (λ = 486 nm) et le rouge (λ = 656 nm) ?
entre les foyers paraxiaux dans le bleu (λ = 486 nm) et le rouge (λ = 656 nm) ? - Le foyer bleu est-il situé, le long de l'axe optique, plus près ou plus loin de la lentille ?
- Quel serait le diamètre de la tache image, considérant ce seul défaut de chromatisme (sans prendre en compte l'aberration sphérique) dans le plan focal paraxial rouge ?
- Comparez l'importance relative de l'aberration sphérique et du chromatisme, dans le cas particulier de cette lentille. Que pouvez-vous prévoir de l'aspect de la tache-image en éclairage polychromatique dans le plan de mise au point rouge ?
- L'écart normal de chromatisme, décrivant l'écart entre la surface d'onde dans le bleu par rapport à une surface d'onde dans le rouge, s'exprime par
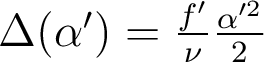 . En utilisant les relations de Nijboer, vérifiez
que l'on retrouve la même expression du diamètre de la tache -image que celle évaluée ci-dessus (4).
. En utilisant les relations de Nijboer, vérifiez
que l'on retrouve la même expression du diamètre de la tache -image que celle évaluée ci-dessus (4).
2. Solution
- ON = 0,15
- ØA = 4,8 µm
-
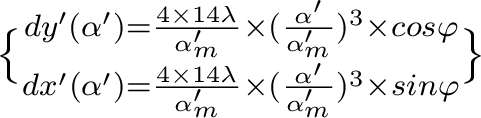
→ attention à l'application correcte des relations de Nijboer, qui font apparaître la dérivée partielle de l'écart normal par rapport à l'ouverture numérique α'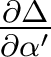 - et non par rapport à l'ouverture numérique normalisée
- et non par rapport à l'ouverture numérique normalisée 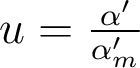
- tache-image à symétrie de révolution, avec un centre lumineux et un fond diffus
- Øm = 439 µm
- Les deux effets se cumulent ! L'aberration sphérique est sensiblement la même à toutes les longueurs d'onde. Dans le plan de mise au point rouge, on observe une tache de diffusion dont le diamètre est proche de la somme des deux contributions,
avec un bord diffus dans le bleu associé à l'aberration sphérique défocalisée à cette longueur d'onde.
La simulation ci-dessous représente le diagramme de points dans le plan de mise au point rouge de la lentille. Le diamètre total est un peu plus faible que celui estimé ici car l'aberration sphérique aux trois longueurs d'onde n'est pas tout à fait aussi forte que celle considérée ici.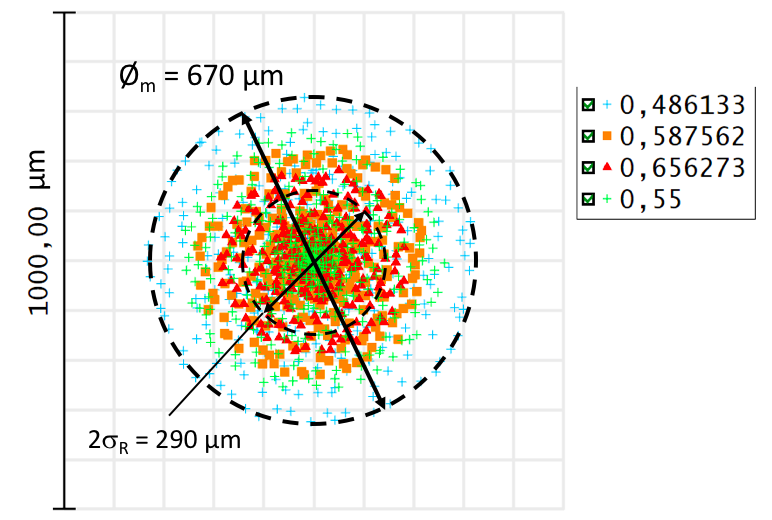
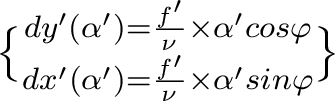 → le diamètre de la tache de diffusion bleue dans le plan de mise au point rouge est
→ le diamètre de la tache de diffusion bleue dans le plan de mise au point rouge est 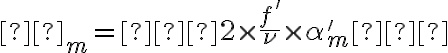 , idem que plus haut.
, idem que plus haut.