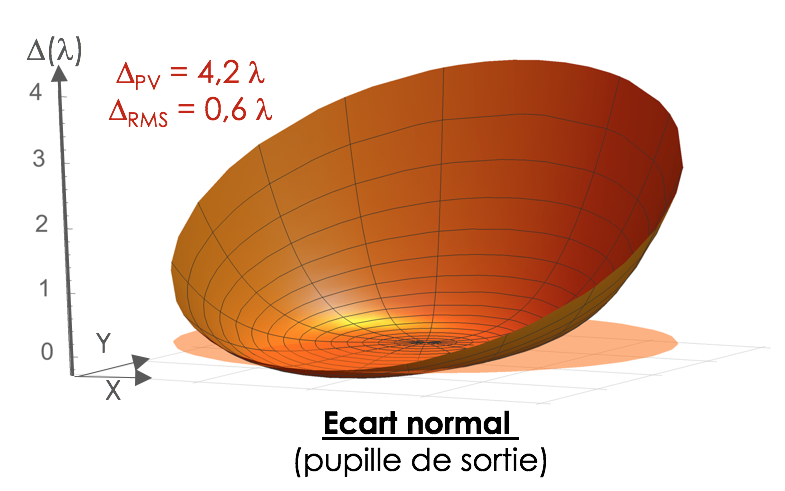
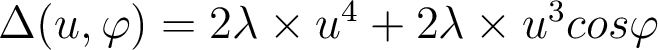Cours n°2 : Ecart normal
Compléments au cours n°2 - démonstrations détaillées sur le théorème de Gouy et les relations de Nijboer
3. Relations de Nijboer
3.2. Exemple
Considérons un dispositif optique travaillant pour une ouverture numérique ON = 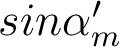 = 0,15 à λ = 780 nm. Pour un point-objet au bord du champ, l'écart normal aberrant évalué par rapport au point-image paraxial est donné par :
= 0,15 à λ = 780 nm. Pour un point-objet au bord du champ, l'écart normal aberrant évalué par rapport au point-image paraxial est donné par :
où 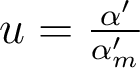 est la hauteur normalisée du rayon dans la pupille.
est la hauteur normalisée du rayon dans la pupille.
Dans l'expression de Δ, le premier terme correspond à de l'aberration sphérique du 3ème ordre, le second à de la coma du 3ème ordre.
L'application des relations de Nijboer à cette expression conduit aux termes d'aberrations transverses suivante, qui donnent l'écart entre l'impact réel des rayons (en fonction de leurs coordonnées 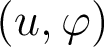 dans la pupille) et la position
de l'image paraxiale dans le plan transverse à l'axe optique :
dans la pupille) et la position
de l'image paraxiale dans le plan transverse à l'axe optique :
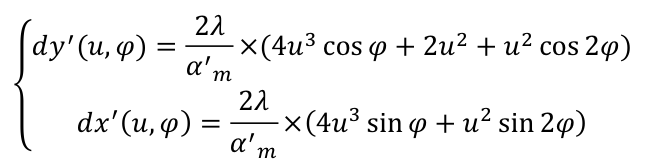
NB : les relations de Nijboer font explicitement apparaître la dérivée partielle de Δ par rapport à l'ouverture numérique α' (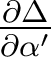 ), et non par rapport à l'ouverture numérique normalisée u
), et non par rapport à l'ouverture numérique normalisée u
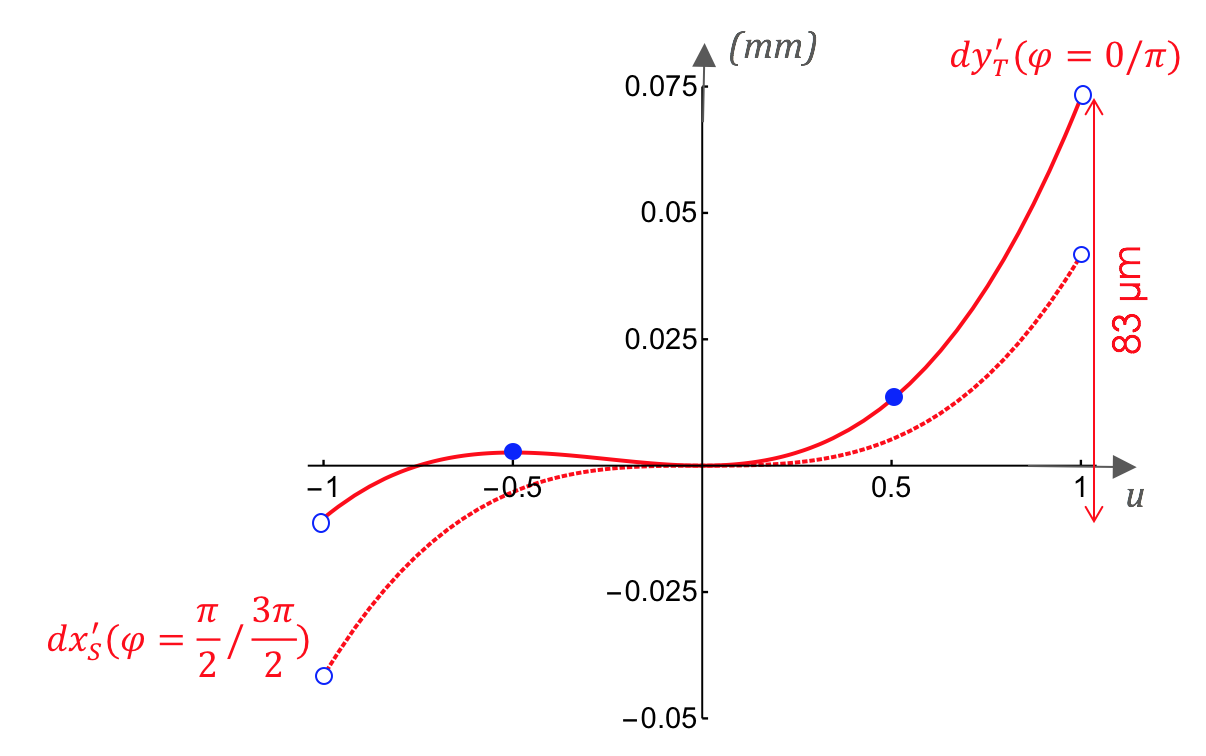
Le tracé de ces coordonnées dans deux plans perpendiculaires (plan tangentiel : 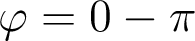 et plan sagittal :
et plan sagittal : 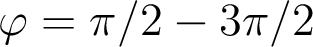 ) permet de quantifier l'importance de la tache image géométrique, c'est-à-dire l'étalement
des points d'impact des rayons dans le plan image paraxial choisi.
) permet de quantifier l'importance de la tache image géométrique, c'est-à-dire l'étalement
des points d'impact des rayons dans le plan image paraxial choisi.
On peut également tracer la répartition des points à partir de ces équations (= "spot-diagramme"), considérant une répartition homogène de rayons dans la pupille :
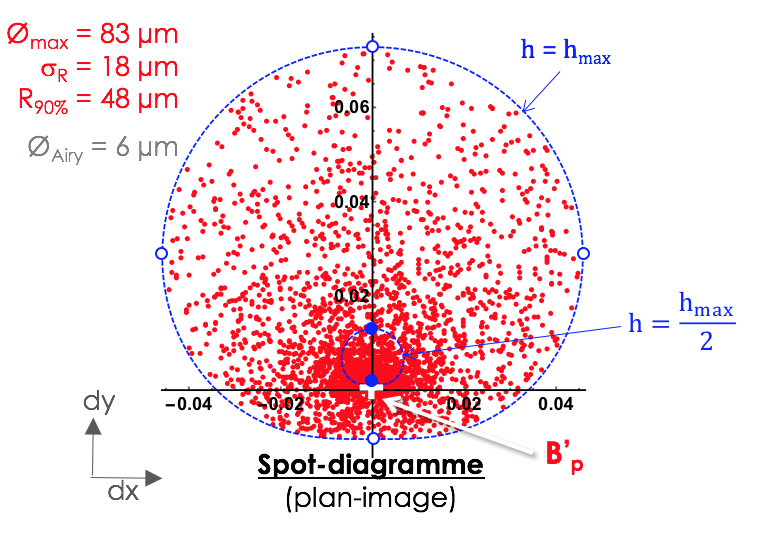
La tache-image présente donc un étalement très important, avec un plan de symétrie 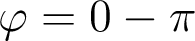 qui est également celui de l'écart normal. Le dispositif étudié est très éloigné de la limite de diffraction, puisque la tache d'Airy
a un diamètre
qui est également celui de l'écart normal. Le dispositif étudié est très éloigné de la limite de diffraction, puisque la tache d'Airy
a un diamètre 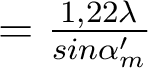 = 6 µm.
= 6 µm.