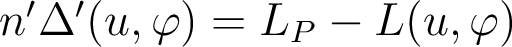Cours n°2 : Ecart normal
| Site: | eCampus |
| Cours: | 7P-138-PHO - Conception de Systèmes Optiques |
| Livre: | Cours n°2 : Ecart normal |
| Imprimé par: | Visiteur anonyme |
| Date: | mardi 10 mars 2026, 11:26 |
Description
Compléments au cours n°2 - démonstrations détaillées sur le théorème de Gouy et les relations de Nijboer
1. Théorème de Gouy
1.1. Démonstration
La démonstration de ce résultat et du sens physique à lui donner peut être faite dans le cas général de la façon suivante :
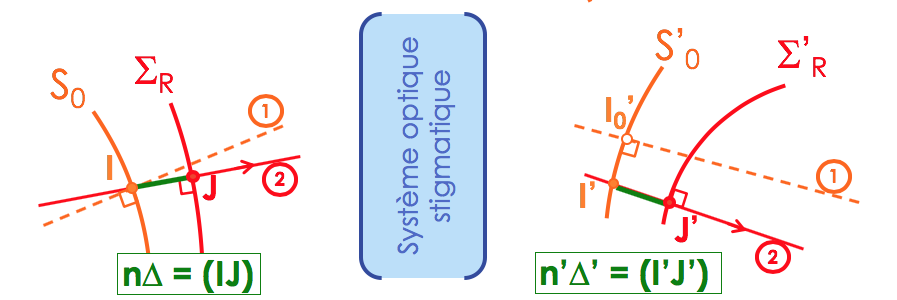
Considérons un système optique stigmatique (c'est-à-dire qu'il n'introduit pas d'aberrations), qui conjugue un point A et un point A' quelconques. Dans le cadre de l'optique paraxiale, une surface d'onde issue de A est sphérique, et une surface d'onde
dans l'espace image centrée sur A' est sphérique également. Ces deux surfaces (S0, S'0) sont les surfaces de référence choisies ici. Le rayon (1) considéré est perpendiculaire au point I à S0, et perpendiculaire
au point I'0 à S'0.
Supposons à présent que la surface d'onde réelle incidente sur le système issue du point A soit aberrante : elle a été générée par un système aberrant quelconque, en amont du système considéré ici. Cette surface réelle ΣR n'est pas sphérique. Le rayon (2) qui passe par le même point I sur S0 est perpendiculaire à ΣR en J, puisque les rayons sont perpendiculaires aux surfaces d'onde (théorème de Malus).
→ par définition, l'écart normal aberrant (nΔ) est le chemin optique (IJ), mesuré le long du rayon réel (2)
.
La surface d'onde Σ'R transformée par le système optique reste aberrante, et est donc également non-sphérique. Suivant la trajectoire du rayon (2) lancé au travers du système, il intercepte la surface de référence S'0 au point
I', et la surface aberrante Σ'R au point J' : l'écart normal aberrant (n'Δ') est le chemin optique (I'J') mesuré le long de ce rayon réel.
→ par définition des surfaces d'onde, les chemins optiques (II'0) et (JJ') sont égaux.
En d'autres termes, la surface d'onde Σ'R est tracée après un temps ∆t égal au temps mis par la lumière pour aller de I en I'0. Les surfaces d'onde S'0 et Σ'R représentent les "photographies" des surfaces d'onde incidentes, respectivement S0 et ΣR, au même instant.
Le chemin optique (IJ') se décompose alors sous la forme :  soit
soit 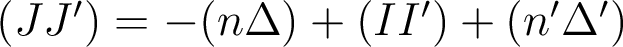 .
.
Or le point I', sur S'0, est proche du point I'0. Toutefois la trajectoire (II'0) n'est pas réellement suivie par la lumière. Alors, d'après le principe de Fermat,
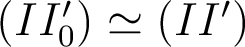 puisque la trajectoire réelle (II') est extrémale. Cette égalité est une approximation, valable au 2ème ordre en
puisque la trajectoire réelle (II') est extrémale. Cette égalité est une approximation, valable au 2ème ordre en  .
.
On en déduit donc que 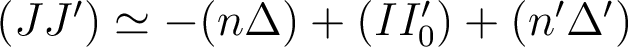 , d'où
, d'où 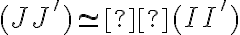 et
et 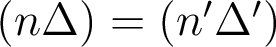 dans le cadre de validité du principe de
Fermat.
dans le cadre de validité du principe de
Fermat.
1.2. Exemples
La conservation de l'écart normal Δ au cours de la propagation en espace libre d'une surface d'onde est l'exemple d'application le plus simple du théorème de Gouy. Cet exemple montre qu'il repose sur le principe de Fermat, et s'appuie sur une approximation dont la limite de validité est illustrée dans le cas d'une lentille simple.
Une seconde démonstration de ce théorème dans le cas de la propagation au travers d'un système non-aberrant est proposée ci-dessous. Le cas particulier traité pour simplifier les schémas (un système afocal travaillant pour un point objet sur l'axe) n'enlève rien à la généralité du théorème.
1.3. Corollaire
Une conséquence du théorème de Gouy est que les chemins optiques aberrants se somment le long du rayon réel : 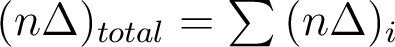
C'est une relation importante, qui permet de comprendre comment il sera possible de compenser les aberrations d'un système optique, en choisissant des composants optiques ayant des aberrations de signes opposés.
→ cf. exemples du cours
2. Écart normal et chemin optique
L'écart normal - plus précisément, le chemin optique aberrant 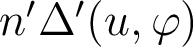 - peut se déterminer numériquement en effectuant la différence entre :
- peut se déterminer numériquement en effectuant la différence entre :
- le chemin optique LP évalué en paraxial entre les points objets et images
- le chemin optique
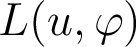 évalue le long d'un rayon réel.
évalue le long d'un rayon réel.
3. Relations de Nijboer
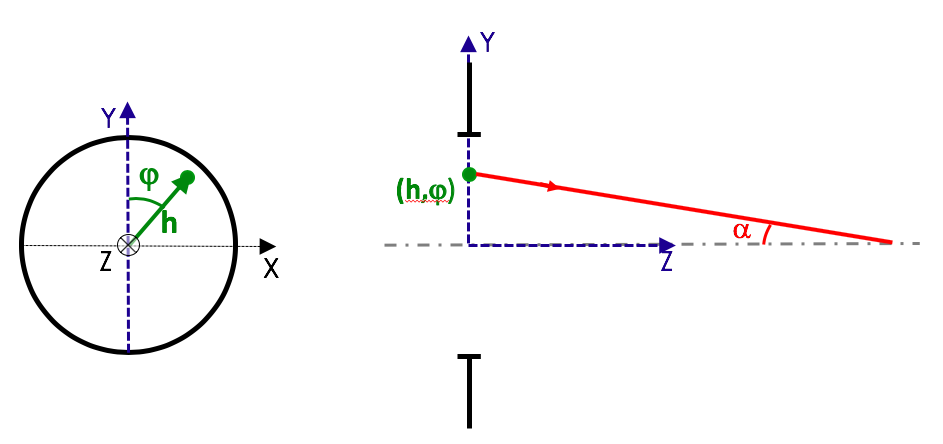
Les relations de Nijboer expriment le lien entre les aberrations transverses (dy', dx') et l'écart normal aberrant ∆.
Elles reposent sur le fait que les rayons optiques sont perpendiculaires à la surface d'onde (théorème de Malus). Ainsi, l'impact des rayons dans le plan-image
considéré est-il directement lié aux dérivées partielles de l'écart normal aberrant par rapport à ses coordonnées dans la pupille.
Dans le système de coordonnées polaires 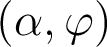 définissant le point d'impact du rayon dans la pupille, les relations de Nijboer s'écrivent :
définissant le point d'impact du rayon dans la pupille, les relations de Nijboer s'écrivent :
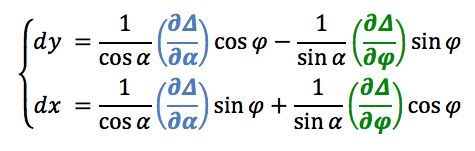
3.1. Démonstration
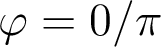 , et suffit à comprendre d'où elle provient.
, et suffit à comprendre d'où elle provient.
3.2. Exemple
Considérons un dispositif optique travaillant pour une ouverture numérique ON = 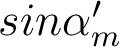 = 0,15 à λ = 780 nm. Pour un point-objet au bord du champ, l'écart normal aberrant évalué par rapport au point-image paraxial est donné par :
= 0,15 à λ = 780 nm. Pour un point-objet au bord du champ, l'écart normal aberrant évalué par rapport au point-image paraxial est donné par :
où 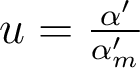 est la hauteur normalisée du rayon dans la pupille.
est la hauteur normalisée du rayon dans la pupille.
Dans l'expression de Δ, le premier terme correspond à de l'aberration sphérique du 3ème ordre, le second à de la coma du 3ème ordre.
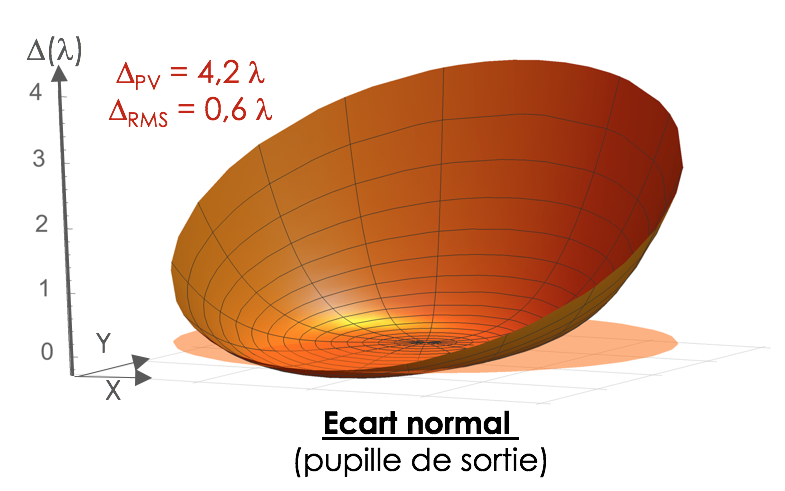
L'application des relations de Nijboer à cette expression conduit aux termes d'aberrations transverses suivante, qui donnent l'écart entre l'impact réel des rayons (en fonction de leurs coordonnées 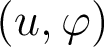 dans la pupille) et la position
de l'image paraxiale dans le plan transverse à l'axe optique :
dans la pupille) et la position
de l'image paraxiale dans le plan transverse à l'axe optique :
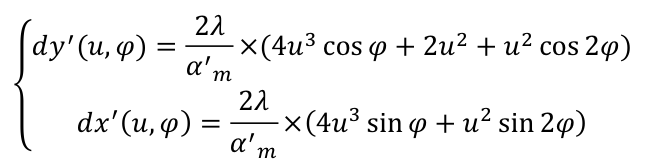
NB : les relations de Nijboer font explicitement apparaître la dérivée partielle de Δ par rapport à l'ouverture numérique α' (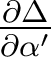 ), et non par rapport à l'ouverture numérique normalisée u
), et non par rapport à l'ouverture numérique normalisée u
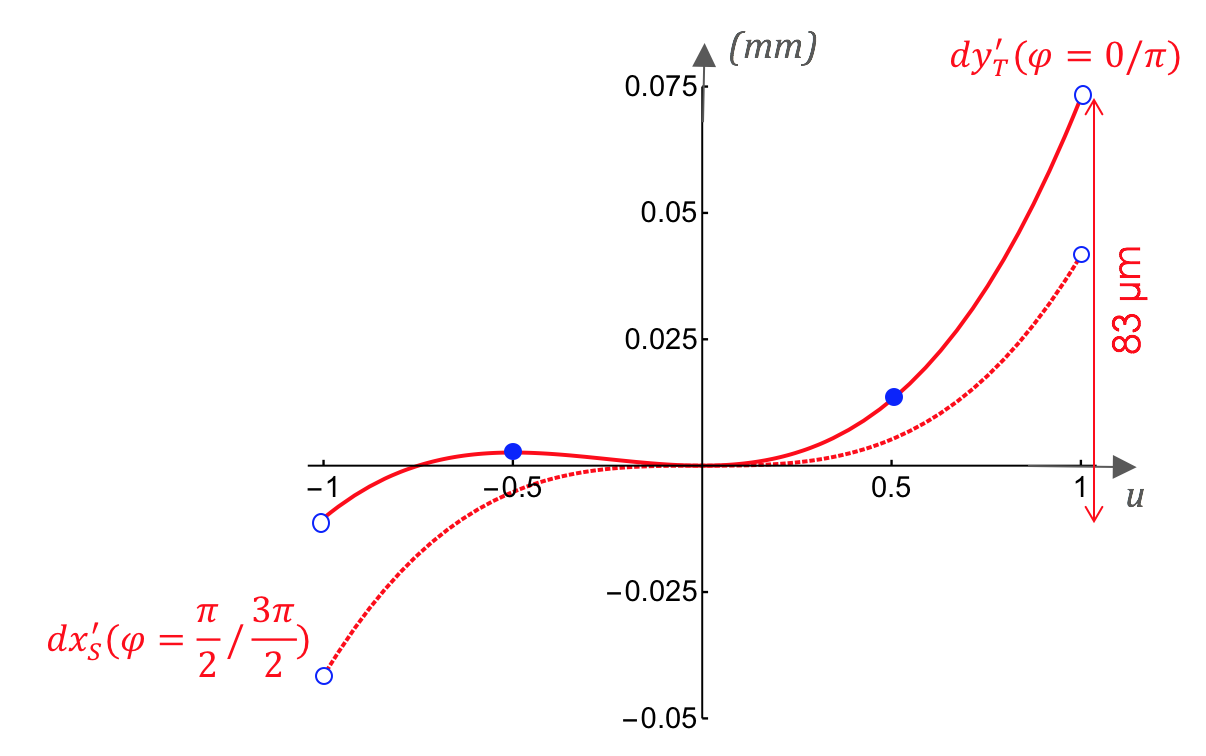
Le tracé de ces coordonnées dans deux plans perpendiculaires (plan tangentiel : 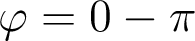 et plan sagittal :
et plan sagittal : 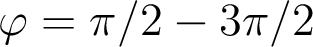 ) permet de quantifier l'importance de la tache image géométrique, c'est-à-dire l'étalement
des points d'impact des rayons dans le plan image paraxial choisi.
) permet de quantifier l'importance de la tache image géométrique, c'est-à-dire l'étalement
des points d'impact des rayons dans le plan image paraxial choisi.
On peut également tracer la répartition des points à partir de ces équations (= "spot-diagramme"), considérant une répartition homogène de rayons dans la pupille :
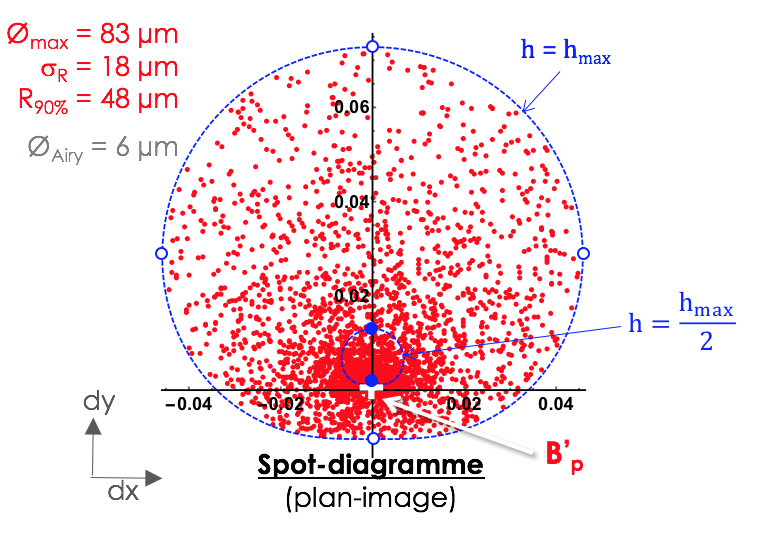
La tache-image présente donc un étalement très important, avec un plan de symétrie 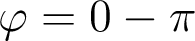 qui est également celui de l'écart normal. Le dispositif étudié est très éloigné de la limite de diffraction, puisque la tache d'Airy
a un diamètre
qui est également celui de l'écart normal. Le dispositif étudié est très éloigné de la limite de diffraction, puisque la tache d'Airy
a un diamètre 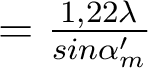 = 6 µm.
= 6 µm.
3.3. Exercice d'application
Évaluation de la tache de diffusion associée à l'aberration sphérique et au chromatisme d'une lentille simple :
cf. Exercice corrigé 'Aberrations sur l'axe d'une lentille simple'
(section Exercices & Quizz)