Cours n°2 : Ecart normal
Requisitos de finalización
Compléments au cours n°2 - démonstrations détaillées sur le théorème de Gouy et les relations de Nijboer
1. Théorème de Gouy
1.3. Corollaire
Une conséquence du théorème de Gouy est que les chemins optiques aberrants se somment le long du rayon réel : 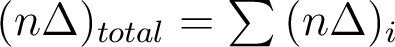
C'est une relation importante, qui permet de comprendre comment il sera possible de compenser les aberrations d'un système optique, en choisissant des composants optiques ayant des aberrations de signes opposés.
→ cf. exemples du cours
