Cours n°2 : Ecart normal

La démonstration de ce résultat et du sens physique à lui donner peut être faite dans le cas général de la façon suivante :

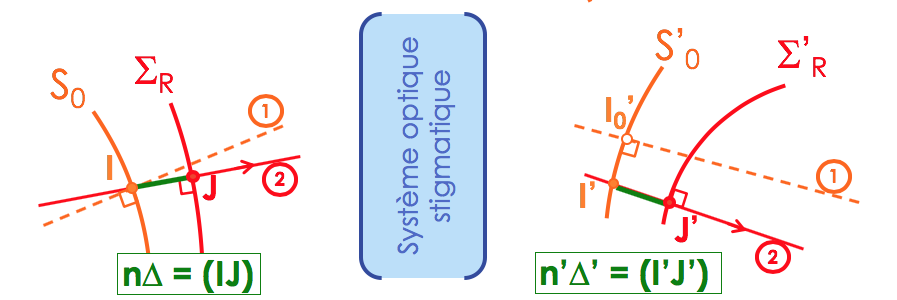
Considérons un système optique stigmatique (c'est-à-dire qu'il n'introduit pas d'aberrations), qui conjugue un point A et un point A' quelconques. Dans le cadre de l'optique paraxiale, une surface d'onde issue de A est sphérique, et une surface d'onde dans l'espace image centrée sur A' est sphérique également. Ces deux surfaces (S₀, S'₀) sont les surfaces de référence choisies ici. Le rayon (1) considéré est perpendiculaire au point I à S₀, et perpendiculaire au point I'₀ à S'₀.

Supposons à présent que la surface d'onde réelle incidente sur le système issue du point A soit aberrante : elle a été générée par un système aberrant quelconque, en amont du système considéré ici. Cette surface réelle Σ_R n'est pas sphérique. Le rayon (2) qui passe par le même point I sur S₀ est perpendiculaire à Σ_R en J, puisque les rayons sont perpendiculaires aux surfaces d'onde (théorème de Malus).

→ par définition, l'écart normal aberrant (nΔ) est le chemin optique (IJ), mesuré le long du rayon réel (2) .

La surface d'onde Σ'_R transformée par le système optique reste aberrante, et est donc également non-sphérique.  Suivant la trajectoire du rayon (2) lancé au travers du système, il intercepte la surface de référence S'₀ au point I', et la surface aberrante Σ'_R au point J' : l'écart normal aberrant (n'Δ') est le chemin optique (I'J') mesuré le long de ce rayon réel.

→ par définition des surfaces d'onde, les chemins optiques (II'₀) et (JJ') sont égaux.

En d'autres termes, la surface d'onde Σ'_R est tracée après un temps ∆t égal au temps mis par la lumière pour aller de I en I'₀. Les surfaces d'onde S'₀ et Σ'_R représentent les "photographies" des surfaces d'onde incidentes, respectivement S₀ et Σ_R, au même instant.

Le chemin optique (IJ') se décompose alors sous la forme : $(JJ') = (JI) + (II') + (I'J')$ soit  $(JJ') =-(n\Delta) + (II') + (n'\Delta')$.

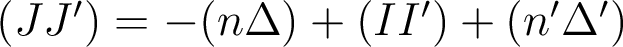Or le point I', sur S'₀, est proche du point I'₀. Toutefois la trajectoire (II'₀) n'est pas réellement suivie par la lumière. Alors, d'après le principe de Fermat, 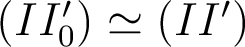$(II'_0) \simeq (II')$ puisque la trajectoire réelle (II') est extrémale. Cette égalité est une approximation, valable au 2^ème ordre en $\delta I' = I'I'_0$.

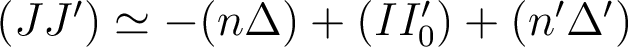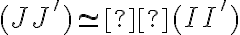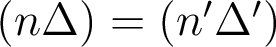On en déduit donc que $(JJ') \simeq -(n\Delta) + (II'_0) + (n'\Delta')$, d'où $(JJ') \simeq  (II')$ et $(n\Delta) = (n'\Delta')$ dans le cadre de validité du principe de Fermat.