M2 AMS - Introduction à l'Analyse Semiclassique

Ce cours présente la quantification semiclassique sur l’espace euclidien, qui débouche sur la construction d’une
classe d’opérateurs linéaires différentiels ou pseudo-différentiels, dépendant d’un petit paramètre (le paramètre de
Planck $0$). L’idée centrale est de faire correspondre à chaque opérateur son “symbole” (une fonction
sur l’“espace des phases”), et de se servir de ce symbole pour analyser l’opérateur. On étudiera les propriétés de
composition de cette famille d’opérateurs, ainsi que l’action induite par l’équation de Schrödinger. On en déduira
quelques propriétés spectrales (distribution des valeurs propres, localisation des fonctions propres), toujours dans le
régime asymptotique 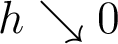$h \searrow 0$ (limite semiclassique). Ce formalisme est apparu initialement en mécanique quantique, il constitue un aspect de l’analyse microlocale utilisée pour analyser plusieurs types d’EDP dans le régime de haute fréquence.