Erratum : liveness analysis
Conditions d’achèvement
We specify a function 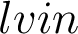 which takes as argument an instruction
which takes as argument an instruction  or a sequence of instructions
or a sequence of instructions  (implemented by 2 different Caml functions) and a set
(implemented by 2 different Caml functions) and a set 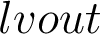 of variables alive at the end of the instructions and computes the variables alive before the instructions.
of variables alive at the end of the instructions and computes the variables alive before the instructions.
We are only considering local variables in the body of a function definition
We have as explained in the document instructions.txt :
| Instruction(s) | livin(i,lvout) |
|---|---|
print( ); ); 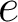 ; ; |
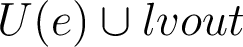 |
return(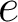 ); ); |
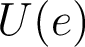 |
x = 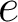 ; ; |
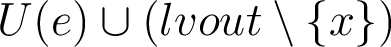 |
| [] | 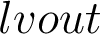 |
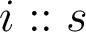 |
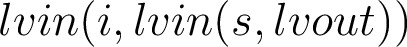 |
if(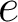 ){ ){ }else{ }else{ } } |
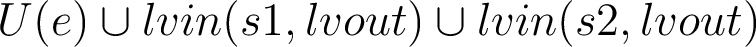 |
The difficulty comes from while loop, the value given in the instructions.txt file is not correct.
The correct value for livin(while(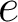 ){
){ },
},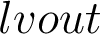 ) is
) is 
- all variables in
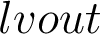 are alive before the while loop is executed because of the execution path where the body of the loop is not executed
are alive before the while loop is executed because of the execution path where the body of the loop is not executed - it is easy to show that the data-flow equation with
 denoting lvin(while(e){s},lvout) is
denoting lvin(while(e){s},lvout) is  . We start the iteration with
. We start the iteration with 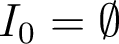 and show that the fixpoint is reached in one pass.
and show that the fixpoint is reached in one pass.
Computing the variables alive in the body of the loop :
- the variables alive after executing the body of the loop are the one alive at the beginning of the loop instruction. So we need to compute
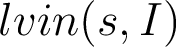 with
with  the set computed above of the variables alive before the loop.
the set computed above of the variables alive before the loop. - we need to be careful on the complexity of the procedure : if we have 3 imbricated loops, and each time we have a loop with body
 we compute both
we compute both 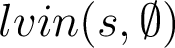 to obtain
to obtain  and then
and then 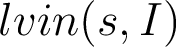 , the fonction lvin will be applied 8 times on the deeper loop body, we will end up with an exponential complexity !
, the fonction lvin will be applied 8 times on the deeper loop body, we will end up with an exponential complexity !
Modifié le: jeudi 2 octobre 2025, 15:18
