En réponse à une question reçue par courriel : "Pourquoi dans cette question (III.20.a) ne considère-t-on pas les termes en u^2 et u ? Est-ce parce qu'on a les coefficients des polynômes de Zernike qui donnent le défocus par rapport au meilleur foyer ? "
À partir de la décomposition du front d'onde sur la base de Zernike donnée dans l'énoncé, il s'agit ici d'exprimer l'écart normal aberrant par rapport à une mise au point paraxiale, le système étant réglé de manière paraxiale (c'est-à-dire que les foyers paraxiaux de l'objectif et de l'oculaire sont confondus pour que le système soit considéré comme afocal en paraxial).
Dans ces conditions, l'écart normal d'aberration sphérique du 3ème ordre ne fait apparaître que des termes en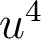 
, les termes en 
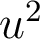exprimant un défaut de mise au point par rapport au foyer paraxial. En d'autres termes, on écrit ici l'écart normal dans la base polynomiale de Seidel, dans laquelle les aberrations apparaissent comme les premiers termes d'un développement limité du système optique par rapport à la description paraxiale. Dans cette base, il n'y a pas de terme en 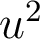si la mise au point est au foyer paraxial pour un point objet sur l'axe. Il suffit donc ici de sommer les contributions de l'écart normal aberrant de chaque optique, par application du théorème de Gouy, en se limitant à la contribution en .
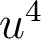Remarquons toutefois que pour un point-objet dans le champ, un terme en 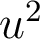dans la décomposition de l'écart normal pourrait apparaître, que l'on pourrait alors associer à de la courbure de champ, c'est-à-dire un défaut de mise au point apparaissant dans le champ par apport au plan image paraxial.
En espérant avoir apporté quelques clarifications à ce sujet,
Gaëlle Lucas-Leclin