Questions & Réponses

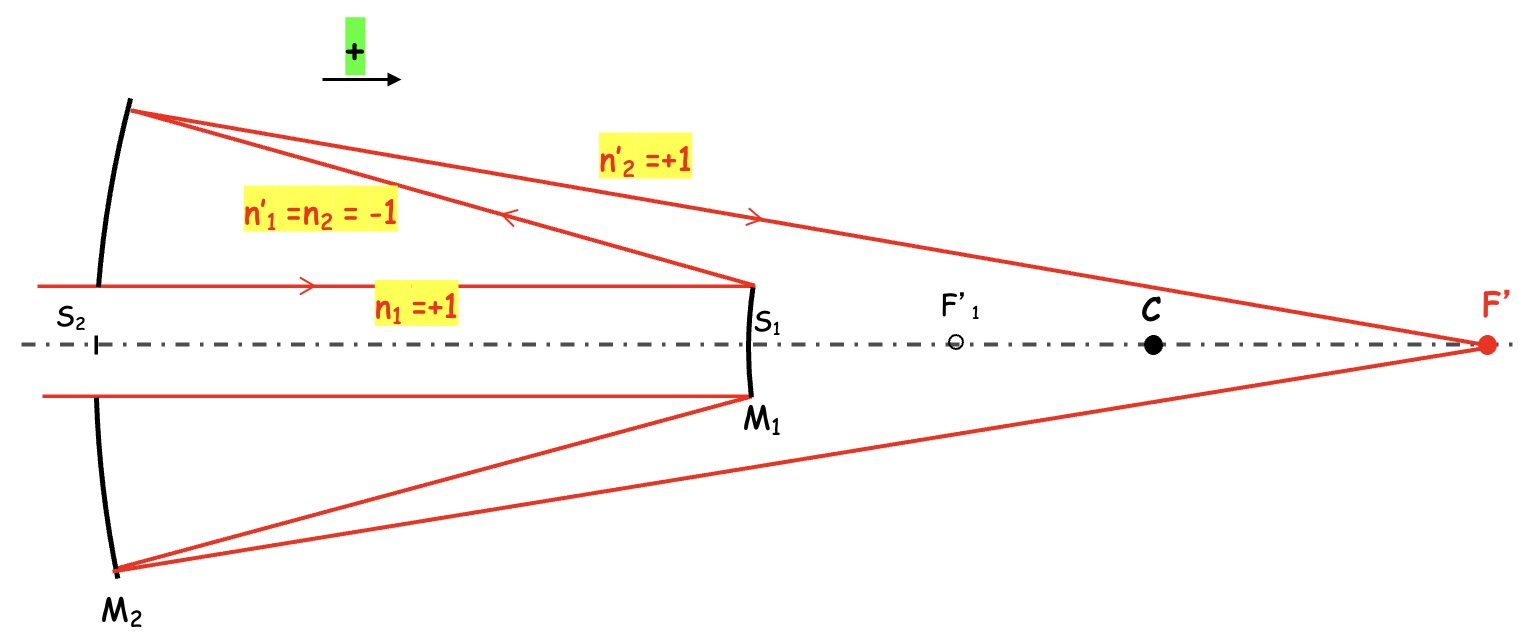
En réponse à un message reçu par courriel au sujet du TD n°4 :

J'ai deux questions au sujet de l'aberration sphérique du système présenté dans le TD 4 (photo ci-dessous). Pouvez-vous m'aider s'il vous plaît ?

- Comment peut-on déterminer le signe de Δ de l'aberration sphérique pour les deux miroirs ? Je ne vois pas quelle surface de référence prendre ;

- Dans la formule de nΔ de l'AS, comment connait-on le signe (et la valeur) de n' et n ? Sont-ils toujours opposés ? 

• L'écart normal aberrant Δ est une grandeur algébrique, c'est une distance dont le signe n'est pas défini dans l'absolu mais dépend du sens positif choisi. Ici, il est naturel de le choisir dans le sens de la gauche vers la droite, c'est-à-dire le sens de propagation de la lumière incidente.
• Les expressions de l'écart normal données pour les dioptres, comme ici, ont pour référence une surface de référence centrée sur l'image paraxiale : le foyer F'₁ pour M₁, le foyer final F' pour M₂.
• Le miroir primaire M₁ est un miroir convexe : c'est une optique divergente, on sait que dans ce cas, l'onde aberrante est en retard par rapport à l'onde de référence (les rayons réels divergent plus que les rayons paraxiaux) : cela correspond, avec le sens positif choisi, à un écart normal positif 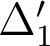$\Delta'_1$ - cf. cours sur la définition de l'écart normal.
• Le miroir secondaire M₂ est un miroir concave, c'est une optique convergente : dans ce cas cas, l'onde aberrante, dans la conjugaison F'₁ --> F', est en avance (les rayons réels convergent plus) : cela correspond, avec le sens positif choisi, à un écart normal 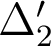$\Delta'_2$ positif.
• Dans le cas particulier des miroirs, les formules des dioptres s'appliquent en considérant que 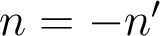$n=-n'$, avec dans l'air 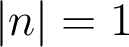$| n | = 1$. Le choix de l'indice initial est donc arbitraire, dès lors qu'il est ensuite maintenu de manière cohérente dans tout le dispositif. Ici, il est naturel de choisir 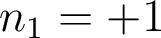$n_1=+1$ et $n'_1=-1$ pour la conjugaison par le miroir M1. Ainsi 
  • Ici, il est naturel de choisir 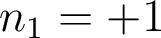$n_1=+1$ et $n'_1=-1$ pour la conjugaison par le miroir M₁
  • Alors, dans l'espace intermédiaire entre les miroirs M₁ et M₂, les relations des de l'écart normal s'écriront avec un indice de l'air n = -1.
  • Finalement, pour respecter cette convention, il faudra écrire pour la conjugaison par le miroir M₂ 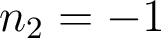$n_2=-1$ et $n'_2=+1$