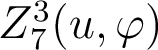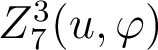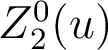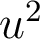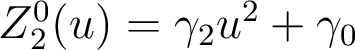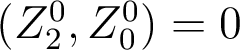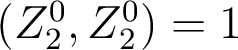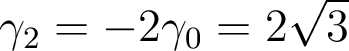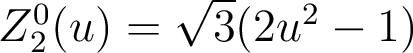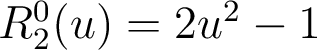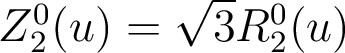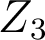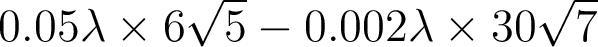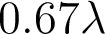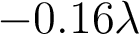Exercices : Polynômes de Zernike (Cours CSO 4)
| Sitio: | eCampus |
| Curso: | 7P-138-PHO - Conception de Systèmes Optiques |
| Libro: | Exercices : Polynômes de Zernike (Cours CSO 4) |
| Imprimido por: | Visiteur anonyme |
| Día: | martes, 10 de marzo de 2026, 11:26 |
Descripción
Exercices d'applications du cours sur les polynômes de Zernike
1. Questions
Répondre aux questions suivantes1.2. Polynôme de Zernike associé au « defocus »
a.
De quels monômes de Seidel 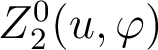 est-il combinaison linéaire ?
est-il combinaison linéaire ?
b. Calculez les coefficients de cette combinaison linéaire en utilisant les relations d’orthogonalité des polynômes
de Zernike.
c.
Retrouvez
directement ces coefficients à partir de la définition des fonctions radiales 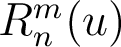 de Zernike.
de Zernike.
1.3. Analyse de front d'onde
La figure ci-dessous résume les résultats
de l’analyse du front d’onde émergent d’une lentille déformable à la longueur d’onde 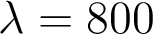 nm.
nm.
La
spécification du fabricant pour la lentille est 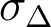 pour une mise au point au meilleur
foyer.
pour une mise au point au meilleur
foyer.
- L’analyse a-t-elle été faite au meilleur foyer ?
- Les résultats de l’analyse sont-ils compatibles avec la spécification du fabricant ?
- Déduire de l’analyse l’amplitude de l’écart normal d’aberration sphérique du 3e ordre, en bord de pupille, pour une mise au point paraxiale.