Cours n°12 : Fonction de Transfert Optique
3. Fonction de transfert pour mire rectangulaire
La fonction de transfert de modulation ( = module de la fonction de transfert optique/incohérente), dans sa définition même, donne accès au contraste de l'image d'une mire d'éclairement sinusoïdal en fonction de sa fréquence spatiale - c'est-à-dire qu'elle s'intéresse à des mires ne contenant qu'une seule fréquence spatiale. Bien qu'une mire sinusoïdale ait une expression analytique très simple, sa réalisation expérimentale est plus complexe. Au contraire, les mires à profil d'éclairement rectangulaire (autrement dit, des traits alternativement noirs et blancs) sont très simples à réaliser, et d'un usage courant pour la caractérisation des dispositifs optiques. C'est pourquoi il est souvent utile de s'intéresser à la fonction de transfert rectangulaire (Square Transfer Function), que les logiciels calculent aisément, et qui est directement comparable aux observations expérimentales.
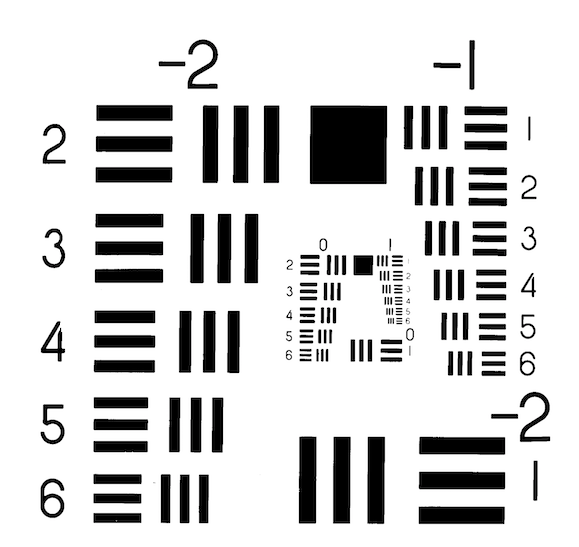
Mire de test à profils rectangulaires (mire USAF de référence)
En effet, l'éclairement d'une mire à profil rectangulaire, de période a, se décompose en série de Fourier :
Il est donc élémentaire d'en déduire l'éclairement de l'image à partir des valeurs de la fonction de transfert 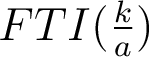 appliquées à chacune des composantes (cf. cours). On peut alors exprimer le contraste de la mire rectangulaire de période a, qui est par définition la FTR à la fréquence spatiale
appliquées à chacune des composantes (cf. cours). On peut alors exprimer le contraste de la mire rectangulaire de période a, qui est par définition la FTR à la fréquence spatiale  :
:
soit
La fonction de transfert rectangulaire donne donc le contraste de l'image de la mire en fonction de sa fréquence fondamentale  . La figure ci-dessous compare les fonctions de transfert en limite de diffraction d'un objectif à pupille circulaire homogène : le contraste de l'image de la mire rectangulaire de période a est supérieur à celui de l'image de la mire sinusoïdale.
. La figure ci-dessous compare les fonctions de transfert en limite de diffraction d'un objectif à pupille circulaire homogène : le contraste de l'image de la mire rectangulaire de période a est supérieur à celui de l'image de la mire sinusoïdale.
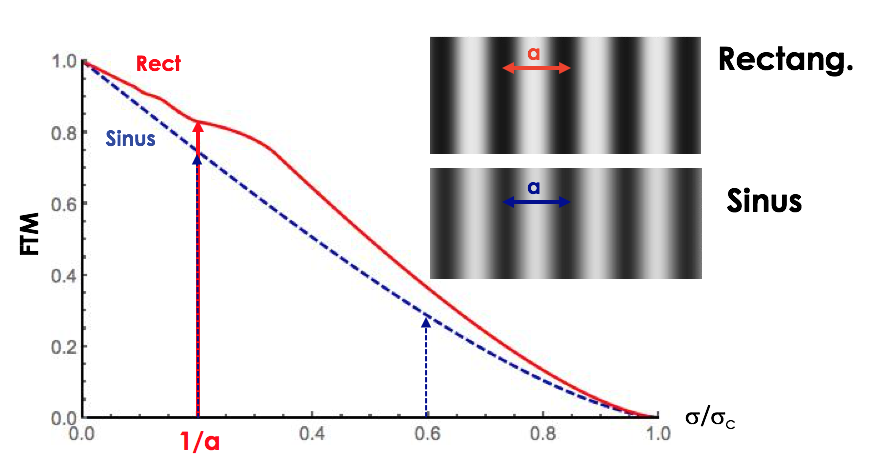
Module des fonctions de transfert pour une mire sinusoïdale et rectangulaire, pour un dispositif optique en limite de diffraction à pupille circulaire homogène
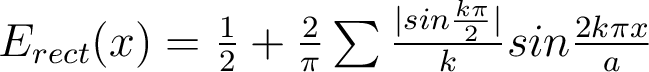
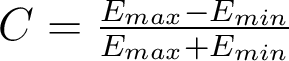
![FT_{Rect}(\frac{1}{a})= \frac{4}{\pi} \sum{\frac{-sin \frac{k\pi}{2}}{k} \times FTM(\frac{k}{a})}= \frac{4}{\pi} \times [FTM(\frac{1}{a})- \frac{1}{3}FTM(\frac{3}{a}) + \frac{1}{5}FTM(\frac{5}{a}) -...] FT_{Rect}(\frac{1}{a})= \frac{4}{\pi} \sum{\frac{-sin \frac{k\pi}{2}}{k} \times FTM(\frac{k}{a})}= \frac{4}{\pi} \times [FTM(\frac{1}{a})- \frac{1}{3}FTM(\frac{3}{a}) + \frac{1}{5}FTM(\frac{5}{a}) -...]](https://ecampus.paris-saclay.fr/filter/tex/pix.php/44c580ad5c5181a89f456e8827a5dc39.png)