Exercices sur l'aberration sphérique (Cours CSO 5)
2. Réponses
Exercice 1
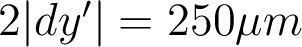
- Diamètre de la tache d'Airy :
 : le système n'est pas limité par la diffraction.
: le système n'est pas limité par la diffraction. 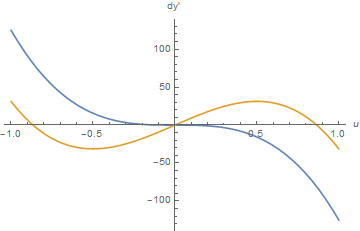
- La courbe de tracé de rayons pour une mise au point au foyer de moindre diffusion s'écrit :
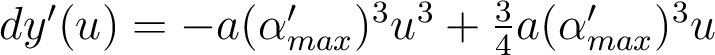
- On égalise
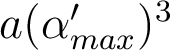 et
et 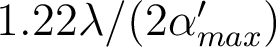 et on obtient
et on obtient 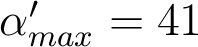 mrad, soit N=12. Cela correspond à la valeur
mrad, soit N=12. Cela correspond à la valeur 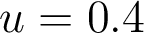 sur le graphe de la question 3.
sur le graphe de la question 3. - Avec cette nouvelle valeur de
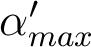 , on trouve
, on trouve 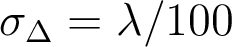 , d'où
, d'où 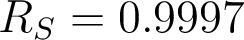 .
.
Exercice 2
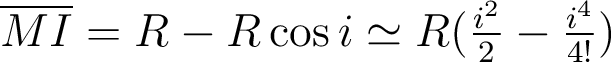 à l'ordre 4 en i.
à l'ordre 4 en i.
Il faut ensuite exprimer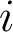 en fonction de
en fonction de 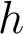 . On a
. On a 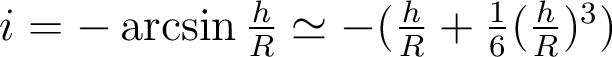 à l'ordre 4 en h.
à l'ordre 4 en h.
On obtient finalement :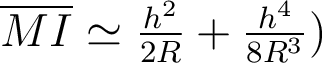 à l'ordre 4 en h.
à l'ordre 4 en h.- La parabole qui approxime au mieux la sphère de rayon R a donc pour équation :
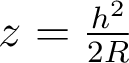
- L'écart entre la sphère et la parabole a le signe de
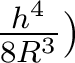 , i.e. positif pour
, i.e. positif pour 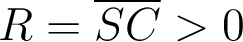 .
. - L'erreur relative commise en confondant la sphère et la parabole est donc :
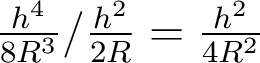 , de l'ordre de 6% pour i=30° (soit
, de l'ordre de 6% pour i=30° (soit 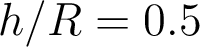 ).
). La parabole est représentée en pointillés, la sphère est en trait plein.
Exercice 3
- La décomposition de l'écart normal
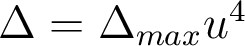 sur les polynômes de Zernike donne
sur les polynômes de Zernike donne ![\Delta=\Delta_{max}[\frac{1}{6\sqrt{5}}Z_4^0 +\frac{1}{2\sqrt{3}}Z_2^0+\frac{1}{3}Z_0^0 ] \Delta=\Delta_{max}[\frac{1}{6\sqrt{5}}Z_4^0 +\frac{1}{2\sqrt{3}}Z_2^0+\frac{1}{3}Z_0^0 ]](https://ecampus.paris-saclay.fr/filter/tex/pix.php/b114f34ebe022fc4c1a541832fef4ee8.png) , d'où
, d'où 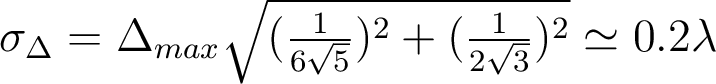 .
.  avec
avec 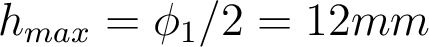
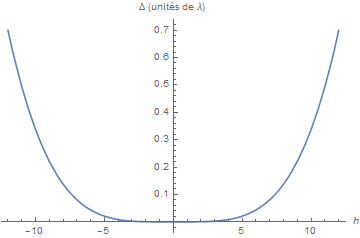
- Les relations de Nijboër vues en cours donnent
 . Ici, il faut adapter cette relation car l'image est à l'infini : l'angle d'ouverture image
. Ici, il faut adapter cette relation car l'image est à l'infini : l'angle d'ouverture image 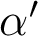 n'est plus une quatité pertinente dans ce cas (il vaut 0) et doit être remplacé par la hauteur d'impact dans la pupille de sortie,
n'est plus une quatité pertinente dans ce cas (il vaut 0) et doit être remplacé par la hauteur d'impact dans la pupille de sortie, 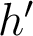 . Et la dimension transverse de la tache aberrante,
. Et la dimension transverse de la tache aberrante, 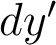 (qui n'est plus pertinente non plus, elle est infinie !), doit être remplacée par une dimension angulaire,
(qui n'est plus pertinente non plus, elle est infinie !), doit être remplacée par une dimension angulaire, 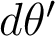 . Et la relation de Nijboër devient :
. Et la relation de Nijboër devient : 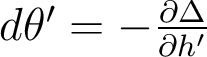 .
.
Pour comprendre cette transformation, on considèrera la configuration générale où l'image se forme à la distance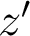 . Les quantités précédentes sont reliées par
. Les quantités précédentes sont reliées par  et
et 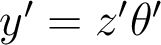 (faites une figure pour vous en convaincre !). Le report de ces relations dans la relation de Nijboër vue en cours conduit bien à
(faites une figure pour vous en convaincre !). Le report de ces relations dans la relation de Nijboër vue en cours conduit bien à  , où le paramètre
, où le paramètre 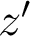 a disparu. Cette relation est donc valable pour
a disparu. Cette relation est donc valable pour 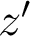 tendant vers l'infini.
tendant vers l'infini.
L'écart normal, pour une mise au point paraxiale, s'écrit :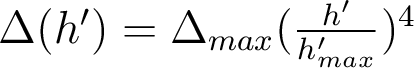 où
où 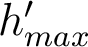 est le rayon de la pupille de sortie. Ici,
est le rayon de la pupille de sortie. Ici, 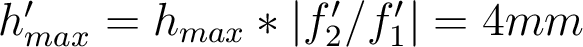 . On en déduit le rayon angulaire de la tache aberrante à l'infini :
. On en déduit le rayon angulaire de la tache aberrante à l'infini : 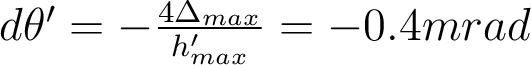 .
. - On va d'abord calculer de combien on doit déplacer la lentille L2 (en valeur absolue), puis on déterminera dans quel sens (par raisonnement). Le déplacement de L2 introduit un terme de courbure sur le front d'onde idéal, noté
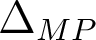 dans le cours (défaut de mise au point). D'après le cours, l'écart aberrant quadratique moyen est minimal lorsque
dans le cours (défaut de mise au point). D'après le cours, l'écart aberrant quadratique moyen est minimal lorsque 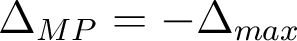 . Par ailleurs,
. Par ailleurs,  où
où 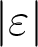 est la quantité dont on déplace la lentille, et
est la quantité dont on déplace la lentille, et 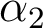 est l'angle d'ouverture objet de la lentille L2 (
est l'angle d'ouverture objet de la lentille L2 (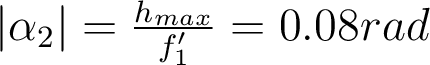 ). On en déduit
). On en déduit 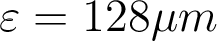 .
.
Pour déterminer le sens du déplacement, on raisonne de la façon suivante : le terme de courbure introduit par le déplacement de L2 doit permettre de réduire l'écart normal pic-vallée. Pour cela, il faut que la partie du front d'onde associée aux rayons paraxiaux, initialement plan, soit divergente après déplacement de L2 (rayon de courbure du front d'onde négatif). Pour que ce soit le cas, il faut rapprocher L2 de L1. - Dans ces conditions, et d'après le cours,
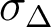 est réduit d'un facteur 4 et devient donc
est réduit d'un facteur 4 et devient donc 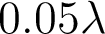 .
.