Imprimir este CapítuloImprimir este Capítulo

Exercices : Polynômes de Zernike (Cours CSO 4)

2. Réponses

  1. Z_7^3(u,\varphi)   est un trèfle à 3 feuilles du 9ème ordre.
  2. a)  Z_2^0(u) est combinaison linéaire de u^2 (defocus de Seidel) et de 1 (piston)
    b) En écrivant que Z_2^0(u)=\gamma_2 u^2 + \gamma_0 , et en reportant dans les relations d'orthonormalité (Z_2^0,Z_0^0)=0 et (Z_2^0,Z_2^0)=1 , on obtient  : \gamma_2=-2\gamma_0=2\sqrt{3} , d'où Z_2^0(u)=\sqrt{3}(2u^2-1) .
    c) La définition des fonctions radiales de Zernike conduit à : R_2^0(u)=2u^2-1 , et ensuite on calcule Z_2^0(u)=\sqrt{3}R_2^0(u) .
     
  3. a) L'analyse n'a pas été faite au meilleur foyer. Si c'était le cas, le coefficient selon Z_3 serait nul (defocus de Zernike). 
         b) On calcule, au meilleur foyer, \sigma_{\Delta}=\lambda\sqrt{0.05^2+0.002^2}\simeq 0.05\lambda , qui vérifie la spécification du fabricant.
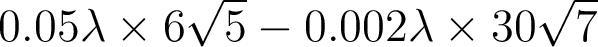
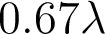
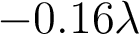
         c) L'amplitude de l'écart normal d'aberration sphérique du 3e ordre, en bord de pupille et pour une mise au point paraxiale, est : 0.05\lambda \times 6\sqrt{5} - 0.002\lambda \times 30\sqrt{7} . Le premier terme vaut 0.67\lambda (il provient de Z_8=Z_4^0 )  et le deuxième terme vaut -0.16\lambda (il provient de Z_{15}=Z_6^0 ).