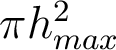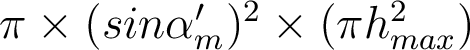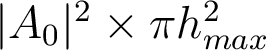Cours n°3 : Réponse percussionnelle
1. Réponse percussionnelle en limite de diffraction
1.2. Maximum d'éclairement
Dans le cas d'une pupille circulaire éclairée de manière homogène, la réponse percussionnelle en limite de diffraction suit le profil suivant :
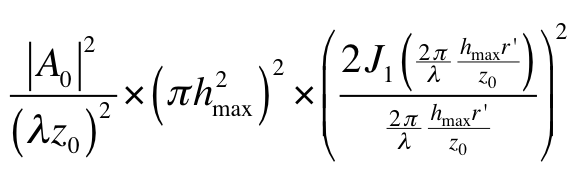
(en reprenant les notations du cours)
Cette expression fait explicitement apparaître l'expression de l'éclairement maximal au centre de la tache d'Airy 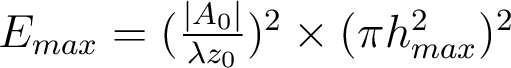 .
.
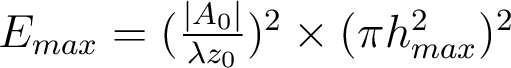 .
. Il est intéressant de remarquer que l'éclairement maximal varie comme la puissance 4 de l'ouverture numérique (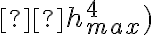 . Ceci découle d'une part du fait que le diamètre de la tache d'Airy diminue, et d'autre part du fait que le flux lumineux récupéré par le système augmente avec
. Ceci découle d'une part du fait que le diamètre de la tache d'Airy diminue, et d'autre part du fait que le flux lumineux récupéré par le système augmente avec 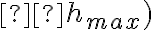 - il est donc "quadruplement" bénéfique de chercher à augmenter l'ouverture numérique d'un système optique ... à condition de pouvoir assurer qu'il travaille en limite de diffraction et ne soit pas limité par les aberrations !
- il est donc "quadruplement" bénéfique de chercher à augmenter l'ouverture numérique d'un système optique ... à condition de pouvoir assurer qu'il travaille en limite de diffraction et ne soit pas limité par les aberrations !
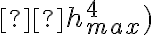 . Ceci découle d'une part du fait que le diamètre de la tache d'Airy diminue, et d'autre part du fait que le flux lumineux récupéré par le système augmente avec
. Ceci découle d'une part du fait que le diamètre de la tache d'Airy diminue, et d'autre part du fait que le flux lumineux récupéré par le système augmente avec 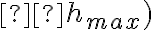 - il est donc "quadruplement" bénéfique de chercher à augmenter l'ouverture numérique d'un système optique ... à condition de pouvoir assurer qu'il travaille en limite de diffraction et ne soit pas limité par les aberrations !
- il est donc "quadruplement" bénéfique de chercher à augmenter l'ouverture numérique d'un système optique ... à condition de pouvoir assurer qu'il travaille en limite de diffraction et ne soit pas limité par les aberrations !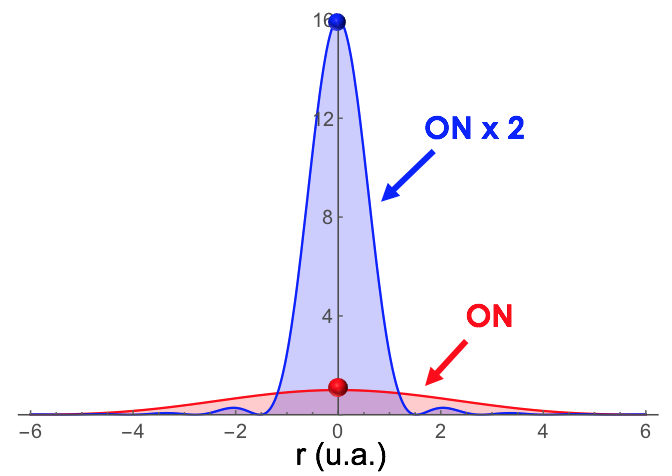
![E_{max}= \frac{|A_0|^2}{\lambda^2} \times [\pi\times (\pi h_{max}^2)\times (sin\alpha'_m)^2] E_{max}= \frac{|A_0|^2}{\lambda^2} \times [\pi\times (\pi h_{max}^2)\times (sin\alpha'_m)^2]](https://ecampus.paris-saclay.fr/filter/tex/pix.php/cfc6fcefc1396179f63d193ba81197ea.png)